Тема 7. Дифференциальное исчисление функции нескольких переменных

Лекция 7.1. Функции нескольких переменных. Частные производные

План:

1.Понятие функции двух и нескольких переменных.

2. Предел и непрерывность функции двух переменных

3. Понятие частных производных и дифференциала функции двух переменных.

Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и вест понятие функции нескольких переменных.

1.Понятие функции двух и нескольких переменных

Пусть задано множество D упорядоченных пар чисел .

Функцией двух переменных называется зависимость f, при которой каждой паре чисел ставиться в соответствие единственное значение переменной . Записывается в виде . При этом x и y называются независимыми переменными (аргументами), а z – зависимой переменной (функцией); символ f означает закон соответствия.

Например, формула, выражающая объем цилиндра является функцией двух переменных где радиус основания, высота.

Областью определения функции называется множество пар при которых функция определена.

Область определения изображается в виде некоторой области на плоскости Линия, ограничивающая данную область, называется границей области. Точки области, не лежащие на границе, называются внутренними точками области. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой и обозначается

Пример. Найти область определения следующих функций:

а) б)

Р ешение. а) Величина, стоящая под знаком квадратного коня должна быть неотрицательной, т.е. Значит, область определения – замкнутый круг с центром в точке и радиусом График функции изображен на рис. 33 и представляет собой поверхность в пространстве – верхнюю полусферу с центром в начале координат и радиусом 2.

Рис. 33

б) то есть область определения вся координатная плоскость.

Функция двух переменных допускает геометрическое изображение.

Графиком функции двух переменных называется множество точек трехмерного пространства , аппликата z которых связана с абсциссой x и ординатой y функциональной зависимостью . Совокупность всех таких точек представляет некоторую поверхность в трехмерном пространстве.

Функция двух переменных – это частный случай функции нескольких переменных. Пусть имеется n переменных величин и каждому упорядоченному набору из некоторого множества X соответствует одно определенное значение переменной y, то говорят, что задана функция нескольких переменных

Переменные называются независимыми переменными (аргументами), а зависимой переменной (функцией).

2. Предел и непрерывность функции двух переменных

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Пусть на плоскости даны две точки и

окрестностью точки называется множество всех точек плоскости, расстояние от которых до точки меньше т.е. Другими словами, окрестностью точки это все точки, лежащие внутри круга с центром и радиусом Обозначают окрестностью точки символом

Число А называется пределом функции при и (или, что тоже самое, при ), если для любого существует такое , что для всех из окрестности точки причем выполняется неравенство

Предел функции обозначается: .

На языке определение предела функции может быть записано следующим образом:

Нахождение предела функции двух переменных задача значительно более сложная, чем нахождение предела функции одной переменной. Задача усложняется из-за того, что для функции двух переменных на плоскости существует бесконечное множество направлений, по которым точка может приближаться к точке В случае функции одной переменной таких направлений всего два: слева и справа. Нахождение некоторых пределов упрощается, если появляется возможность с помощью замены перейти к функции одной переменной.

Пример… Найти

Решение. Положим Очевидно, что если и то

Тогда

Из определения предела функции следует, что если предел функции в точке существует, то он не должен зависеть от пути, по которому точка приближается к точке Если зависимость от пути появляется, то предела функции в точке не существует. Поясним это на примере.

Пример… Найти

Решение. Выберем направление, по которому будем приближаться к точке Пусть приближение будет проходить по прямой где некоторое число. Тогда

Таким образом, предел зависит от величины k, т.е. от направления, по которому точка приближается к точке Следовательно, функция в точке предела не имеет.

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.

Функция называется непрерывной в точке если предел функции в этой точке существует и равен значению функции в этой точке:

Иначе говоря, функция непрерывна в точке если она:

1. определена в этой точке и некоторой ее окрестности;

2. существует конечный предел ;

3. выполнено равенство

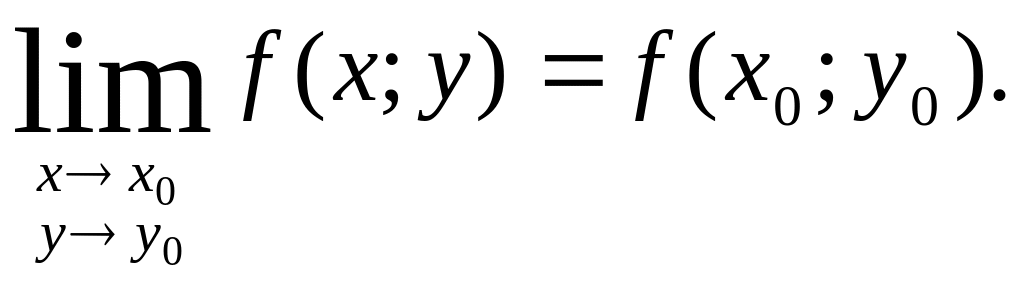
Функция непрерывна в области, если она непрерывна во всех точках этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке, а именно в этой точке либо функция не определена, либо не существует предела, либо значение функции не равно значению предела) называются точками разрыва этой функции. Например, для функции точками разрыва являются точки прямой (их называют линиями разрыва).

Для функций двух переменных справедливы теоремы о непрерывных функциях одной переменной.