2.1.2 Методика расчета коэффициента теплопроводности

В работе применялась написанная методика по определению коэффициента теплопроводности.

Поток тепла через тело с тепловым сопротивлением R_s пропорционален разности температур между границами тела ΔТ:

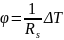(2.1)

Тепловое сопротивление тела R_s определяется коэффициентом теплопроводности материала и геометрии тела

(2.2)

Здесь λ- коэффициент теплопроводности, А- площадь поперечного сечения и h – длина тела. Для цилиндрического образца с диаметром D:

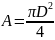(2.3)

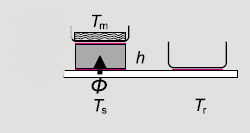
Рисунок 2.3 - Схема размещения исследуемого образца на датчике ДСК анализатора. h - высота цилиндрического образца;φ - тепловой поток из датчика в образец; Т_m - температура расплавленного металла; T_s - температура датчика под образцом; T_r - температура образца сравнения.

В качестве образца сравнения используется пустой тигель. Точно такой же тигель с чистым металлом помещается на образец цилиндрической формы. Зазоры между тигелем, образцом и датчиком заполняются теплопроводящим маслом. На рис.2.3 показана схема эксперимента для определения коэффициента теплопроводности материала методом ДСК. Величина потока тепла от датчика анализатора к металлу на верхней поверхности образца зависит не только от теплового сопротивления самого образца, но и теплового сопротивления границ датчик – образец (R₁) и образец – металл (R₂). Поэтому формула (2.1) должна быть переписана в следующий вид:

(2.4)

Что бы обеспечить воспроизводимость величин R₁ и R₂ зазоры на границах заполнялись теплопроводящим маслом. В этих условиях можно считать, что при использовании образцов с одинаковым поперечным сечением величины R₁ и R₂ не зависят от образца и вводился параметр

R_Т = R₁ + R₂ (2.5)

R_s , а значит и искомый коэффициент теплопроводности образца может быть определен только при условии, что известны входящие в уравнения (2.4) и (2.5) величины . Поскольку используется чистый металл, величина во время плавления известна. Величины определяются ДСК анализатором в ходе измерения, а величина 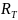может быть найдена из серии измерений. Если оказывается много меньше R_s, то им можно пренебречь [24].

В этом случае для определения λ достаточно снять всего одну кривую плавления.

(2.6)

Подставив уравнение (2.2) в выражение (2.1), получим формулу (2.6). Формула (2.6) справедлива только в ходе плавления. В этом случае ΔТ равно разности температур Т_s в момент времени t и точки плавления металла ( т.е. температуры начала плавления).

(2.7)

Соответствующий тепловой поток φ дает разность теплового потока в момент времени t и потока в начале плавления.

Таким образом, S представляет собой угловой коэффициент линейного участка пика плавления. Из уравнений (2.4)-(2.7) получаем:

(2.8)

Проведя измерения для двух образцов из одного материала с разными высотами цилиндра можно рассчитать величину λ по уравнению 2.9.

(2.9)

где Δh=h₂ –h₁ есть разность высот цилиндров, S₁-угловой коэффициент кривой ДСК для меньшего образца и S₂ - для большего образца. Если провести измерения для нескольких цилиндров с разными высотами, из линейных выражений 1/S и h/А уравнения (2.8), можно определить коэффициент теплопроводности [25].