Линейная засечка
В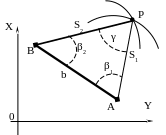
линейной засечке исходными данными
являются координаты пунктов А и В;
измеряемыми данными являются расстояния
и
(относительная ошибка измерения
расстояний
);
определяемые данные – координаты
точки P.
Рисунок 33 – Линейная засечка
Графическое решение.
Сначала на чертеже (плане) нужно построить систему координат и нанести точки Α и Β по их известным координатам; затем нужно провести две окружности с центрами в точках Α и Β, первую окружность – радиусом и вторую – радиусом ; одна из точек пересечения этих окружностей и является искомой точкой Р; другая точка P’ является является вторым (альтернативным) вариантом решением засечки (рис.33)
Аналитическое решение линейной засечки может быть выполнено по двум алгоритмам: первый из них предусматривает решение системы уравнений двух измеренных расстояний
,
.
У этой системы уравнений нет простого решения в системе координат , поэтому приходится применять систему координат с началом в точке А и осью , направленной от точки А вдоль линии АВ. В новой системе координаты точек А и В будут равны
Расстояние , равное длине линии АВ, находится из решения обратной геодезической задачи между точками А и В; при этом вычисляется также дирекционный угол линии АВ.
Уравнения двух окружностей в новой системе координат будут иметь вид
;
.
Совместное решение этих двух уравнений предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого
,
откуда
,
и
.
Если искомая точка находится слева от линии АВ, то в формуле для нужно брать знак “минус”, если справа, то – знак “плюс”.
Пересчёт координат точки из системы в систему выполняется по формулам
,
.
Описанный алгоритм удобен для составления программы при решении линейной засечке на ЭВМ.
Алгоритм “ручного счёта” предусматривает решение треугольника АВР по формулам планиметрии:
в треугольнике ABР по теореме косинусов вычислить углы β1 и β2
,
;
- вычислить угол
γ этого же треугольника
;
вычислить дирекционные углы сторон AР и BР:
точка Р справа от линии AB
,
;
точка Р слева от линии AB
,
;
дирекционный угол αAB следует
взять равным углу α из решения обратной
геодезической задачи между точками A
и B;
;
- решить прямые геодезические задачи:
из пункта A на точку P
,
,
и из пункта B на точку P
,
;
расхождение координат
и
по двум решениям не должно превышать
0,02 м;
вычислить ошибку положения точки P по формуле
.
Пример решения линейной засечки приведён в таблице 7.
Напоминание: При выполнении операций
19 и 20 искомый угол (β1 или β2)
следует перевести из десятичной формы
в полную форму, округлить до целых секунд
и затем уже записать в таблицу вычислений.
Перед выполнением операций 23 и 24 нужно
перевести в десятичную форму угол
;
перед выполнением операций 25 и 26 нужно
перевести в десятичную форму угол
.
Таблица 7 - Решение линейной засечки
№ п/п |
Обозначения (точка Р справа от линии АВ) |
Вычисления |
5 8 9 10 11 12 |
b (м) S1 S2 (справа) b2 S12 S22 |
1 499, 78 1 000, 00 1 200, 00 2 249 340 1 000 000 1 440 000 |
13 14 15 |
b2 + S12 − S22
Cos β1 = (13) / (14) |
1 809 340 2 999 560 + 0, 603 202 |
6 19 21 |
αAB β1 = arcos (15) αAP = (6) + (19) |
3040 07’ 08” 52 54 02 357 01 10 |
1 23 27 28
24 2 |
XA (м)
X2 = (1) + (23) Y2 = (2) + (24)
YA |
6 643 000, 00 + 998, 65 6 642 998, 65 7 374 948, 00
− 52, 00 7 375 000, 00 |
16 17 18 |
b2 + S22 − S12
Cos β2 = (16) / (17) |
2 689 340 3 599 472 + 0, 747 148 |
7 20 22 |
αBA = αAB ± 1800 β2 = arcos (18) αBP = (7) − (20) |
1240 07’ 08” 41 39 22 82 27 46 |
3 25 29 30
26 4 |
XB (м)
X = (3) + (25) Y = (4) + (26)
YB |
6 642 841, 24 + 157, 40 6 642 998, 64 7 374 948, 00
+ 1 189, 63 7 373 758, 37 |
31 |
|
850 26’ 36” |
32 |
MP (м) |
0, 16 |
