4.2.5. Прямая угловая засечка

Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы и измеряются на двух пунктах с извест­ными координатами, каждый от своего направления с известным дирекционным углом (рис.30 ).

Исходные данные: ;

Измеряемые элементы: ;

Неизвестные элементы: точки .

Если или не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D .

Графическое решение. От направления AC отложить с помощью транспортира угол и провести прямую линию AP; от направления BD отложить угол и провести прямую линию BP ; точка пересече­ния этих прямых является искомой точкой P.

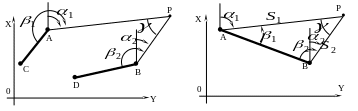
Рисунок 30 – Общий случай прямой угловой засечки Рисунок 31 – Частный случай ПУЗ

Аналитическое решение. Приведем алгоритм, соответ­ствующий общему случаю засечки:

1) вычислить дирекционные углы линий AP ( ) и BP ( )

; ;

2) написать два уравнения прямых линий

для линии АР ,

для линии ВР ;

3) решить систему двух уравнений и вычислить неизвестные коор­динаты

,

.

Частным случаем прямой угловой засечки считают тот случай, когда углы и измерены от направлений AB и BA, причем угол - правый, а угол - левый (в общем случае засечки оба угла - левые) - рис.31.

Решение прямой угловой засечки методом треугольника соответ­ствует частному случаю засечки. Порядок решения прямой угловой засечки методом треугольника:

1) решить обратную задачу между пунктами A и B и получить дирекционный угол и длину линии AB,

2) вычислить угол при вершине P ;

3) используя теорему синусов для треугольника APB

,

вычислить длины сторон AP ( ) и BP ( ) ;

4) вычислить дирекционные углы и

, ;

5) решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P ; оба решения должны совпасть.

Для вычисления координат в частном случае прямой угловой засечки можно использовать формулы Юнга

,

.

От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геоде­зическую задачу между пунктами A и B и получить дирекционный угол линии AB и затем вычислить углы в треугольнике APB при вершинах A и B

и .

Для машинного счета все рассмотренные способы решения прямой угловой засечки по разным причинам неудобны. Один из возможных алгоритмов решения общего случая засечки на ЭВМ предусматривает следующие действия:

1) вычисление дирекционных углов и ,

2

P

) введение местной системы координат с началом в пункте A и с осью , направленной вдоль линии AР, пересчет координат пунктов A и B и дирекционных углов и из системы в систему (рис.32)

; ; ; ;

;

.

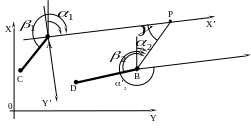
Рисунок 32 – Прямая угловая засечка в системе координат

3) запись уравнений линий AP и BP в системе

,

;

и совместное решение этих уравнений

,

; (3.2)

4) перевод координат и из системы в систему

,

.

Так как и угол засечки всегда больше , то решение (3.2) всегда существует.