4.2.3. Полярная засечка

В полярной засечке исходными данными являются координаты пункта A и дирекционный угол направления AB (или координаты пункта B), измеряемыми элементами являются горизонтальный угол β (средняя квадратическая ошибка измерения угла mβ) и расстояние S (относительная ошибка его измерения mS/S = 1/T), неизвестные элементы – координаты X, Y точки P (рис. 28).

Исходные данные: XA, YA, αAB.

Измеряемые элементы: β , S .

Неизвестные элементы: X , Y .

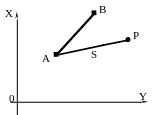
Рисунок 28 – Схема полярной засечки

Вычислим дирекционный угол направления АP и запишем два уравнения, соответствующие двум элементарным измерениям: уравнение прямой линии, проходящей через точку А в заданном направлении АP, и уравнение окружности радиусом с центром в точке А.

Алгоритм решения полярной засечки в кратком виде:

- вычислить дирекционный угол линии AP ;

- вычислить приращения координат: ; ;

- вычислить координаты точки P: ; ;

- вычислить ошибку положения точки P: ; ρ=206265”.

Пример решения полярной засечки приведён в таблице 4.

Таблица 4 - Решение полярной засечки

№ п/п	Обозначения	Вычисления
3 4	αΑΒ β	3040 07’ 08” 34 12 30
6 6’	αΑP αΑP (десятичная форма)	338 19 38 338. 327 222
7 8 5	Sin αΑP Cos αΑP S (м)	− 0. 369 305 + 0. 929 308 1 000.00
1 9	XA (м)	6 642 000.00 + 929.31
11 12	XP YP	6 642 929.31 7 374 630.70
10 2	YA (м)	− 369.30 7 375 000.00
13	MP (м)	0.17

4.2.4. Прямая и обратная геодезические задачи

В геодезии есть две стандартные задачи: прямая геодезичеcкая задача на плоскости и обратная геодезическая задача на плоскости.

Прямая геодезическая задача - это вычисление координат , второго пункта, если известны координаты , первого пункта, дирекционный угол и длина линии, соединяющей эти пункты.

Прямая геодезическая задача является частью полярной засечки, и формулы для ее решения берутся из набора формул для решения полярной засечки

,

.

Обратная геодезическая задача - это вычисление дирекционного угла и длины линии, соединяющей два пункта с известными координатами и (рис.29).

Рисунок 29 – Схема обратной геодезической задачи

Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна   ; катеты равны приращениям координат точек 1 и 2 ( ), а один из острых углов равен румбу   линии 1-2.

Если   и  , то треугольник решается по известным формулам

;

и .

Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому

.

Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:

- определение номера четверти по знакам приращений координат ;

- вычисление дирекционного угла по формулам связи дирекционного угла и румба в соответствии с номером четверти.

Контролем правильности вычислений является выполнение равенства

.

Если , то ,

при ;

при .

Если , то ,

при ;

при .

Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль при :

,

,

если , то ;

если , то .

Таблица 5 – Решение обратной геодезической задачи (1-й алгоритм)

№ п/п	Обозначения	Вычисления
3 1 5	XB (м) XA XB – XA	6 642 841.24 6 642 000.00 + 841.24
13 11	b = (5) / (11) Cos α	1 499.78 + 0. 560 910
7 8 8’ 9	tg r r (десятичная форма) r (IY четверть) α = 3600 – r	1. 475 952 55. 881 229 550 52’ 52” 3040 07’ 08”
10 12	Sin α b = (6) / (10)	− 0. 827 877 1 499.78
4 2 6	YB (м) YA YB − YA	7 373 758.37 7 375 000.00 − 1 241.63
14 15 16 17	(XB – XA)2 (YB − YA)2 b2 = (14) + (15) b = √ (16)	707 684.7 1 541 645.0 2 249 329.7 1 499.78

Таблица 6 – Решение обратной геодезической задачи (2-й алгоритм)

№ п/п	Обозначения	Вычисления
3 1 5	XB (м) XA XB – XA	6 642 841.24 6 642 000.00 + 841.24
11 12 12’ 13	Cos a’ = (5) / (10) a’ (десятичная форма) a’ α = 3600 – a’	+ 0. 560 909 55. 881 316 550 52’ 53” 3040 07’ 07”
4 2 6	YB (м) YA YB − YA	7 373 758.37 7 375 000.00 − 1 241.63
7 8 9 10	(XB – XA)2 (YB − YA)2 b2 = (14) + (15) b = √ (16)	707 684.7 1 541 645.0 2 249 329.7 1 499.78