8.1. Сущность измерения расстояний подвесным мерным прибором

Сущность измерений расстояний подвесными мерными приборами сводится к измерению длины хорды АВ = l₀ (рис. 57) с помощью дуги АВ = s цепной линии, которую образует свободно висящая гибкая нерастяжимая тяжелая нить, удерживаемая в равновесии приложенными к ее концам равным силами F (точки А и В лежат на одном уровне). Длина стягивающей хорды мерного прибора при его горизонтальном положении может быть представлена приближенно в виде

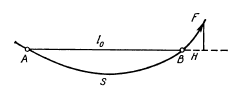
Рис. 57. Схема измерения длины подвесными приборами

где s – длина цепной линии;

p - вес единицы длины мерного прибора;

H - горизонтальная составляющая силы натяжения мерного прибора.

Если p и H постоянны, и величина хорды l₀ будет постоянна. Растяжение мерного прибора под действием силы F будет равно

где σ - растяжение единицы длины мерного прибора под влиянием веса p,

Длина l₀ хорды АВ при положении точек А и В на одной высоте будет согласно формуле (8.1) равна

Формула (8.2) дает нормальную длину хорды при горизонтальном ее положении и натяжении р , называемую длиной мерного прибора.

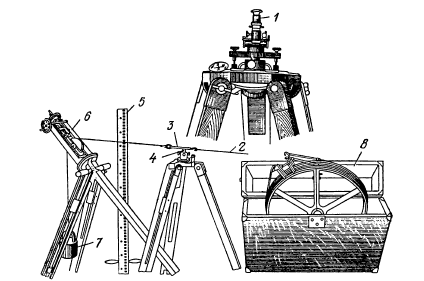
Рис. 58. Базисный прибор БП-2

При измерении расстояний по шкалам производят отсчеты. Если обозначить отсчет по передней шкале буквой П, а по задней буквой 3, то длину интервала, измеренного проволокой, можно подсчитать по формуле

При компарировании на каждый мерный прибор выдается свидетельство, в котором выписывается уравнение прибора при температуре t₀

где l - длина мерного прибора при температуре t и натяжении, равном 10 Н;

l₀ = 24 м - номинальная длина мерного прибора;

∆l – поправка за компарирование при темпера-туре t;

α и β - термические коэффициенты расширения прибора.

8.2. Измерение линий светодальномером

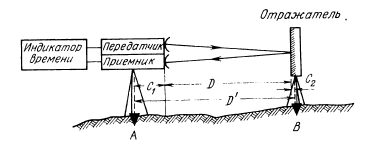
Рис. 59. Схема измерения расстояния

при помощи светодальномера

В момент t₁ передатчик, расположенный в пункте А (рис. 59), излучает в направлении к пункту В электромагнитные волны в виде отдельного импульса который затем отражается и в момент времени t₂ приходит обратно в пункт А. полагая при этом, что электромагнитные волны распространяются прямолинейно

И з формулы (8.4) для определения относительной ошибки измерения расстояний найдем

где τ = t2 – t1;

mD, mv, mτ - средние квадратические ошибки опре-деления величин D, v и τ соответственно.

Найдем с какой ошибкой должны быть определены величины v и τ, если требуется измерить линию длиной D = 1 км с относительной ошибкой 1:400 000 (m = 2,5 мм). Применим к формуле (8.5) принцип равных влияний

Измерение времени τ может быть выполнено на основе двух методов:

а) при помощи излучения импульсов и приема их после отражения (импульсный или непосредственный метод);

б) по разности фаз посылаемых и принимаемых модулированных колебаний (фазовый, или косвенный, метод).

Гармонические колебания какой-либо величины определяются уравнениями вида

в которых А амплитуда колебаний; ω - угловая или круговая частота; t - время. Величина ωt называется фазой колебания. Фазы, отличающиеся друг от друга на величину 2Nπ, (где N = 0, 1, 2, 3, ...), будут одинаковыми. Фазы, отличающиеся друг от друга на нечетное число величин π, называются противоположными

к олебания происходят в противоположных фазах. Для любой точки на прямой можно написать

где v - скорость распространения колебаний в окружающей среде, образуя волновое поле;

φ₀ - начальная фаза в момент времени t = 0.

Выражение вида (8.8) называется уравнением плоской волны гармонического колебания. Колебания высокой частоты характеризуются тремя параметрами: амплитудой, частотой и начальной фазой. Процесс изменения указанных параметров называется модуляцией, она разделяется на амплитудную, частотную и фазовую.

На рис. 60 условно показано распространение колебаний в пространстве вдоль некоторой прямой для двух моментов времени - t₁ и t₂.

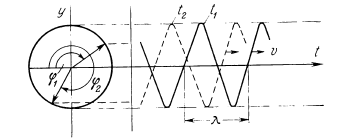
Рис. 60. Схема распространения колебаний

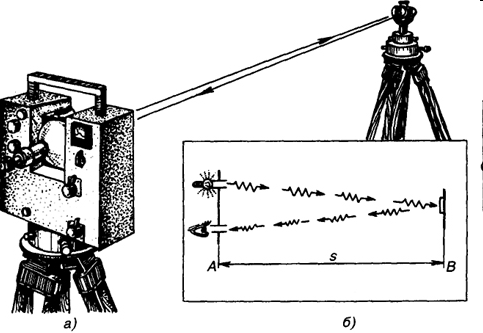
Рис. 61. Светодальномер (а) и ход лучей (б)

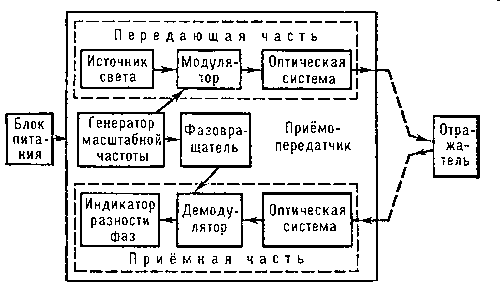
Рис. 63. Блок-схема электрооптического дальномера