7.7. Расчет точности измерения угла в полигонометрическом ходе

Рассмотрим случайный характер влияния. Возьмем вытянутый полигонометрический ход, в котором углы предварительно исправлены за угловую невяз-ку. Для этого хода средняя квадратическая ошибка поперечного сдвига равна

и ли

Переходя к предельным ошибкам, получим

Для каждого источника ошибок случайного характера следует величину пред ∆ β_случ уменьшить в √ 6 раз, т. е.

Если источник ошибок имеет систематический характер, то для расчета его влияния используем соотношение (6.20)

П олагая, что измерения равноточны, т.е. dβ1 = dβ2= . . . = dβn = dβ и s1= s2 = . . . = sn= s, будем иметь

о ткуда

С учетом того, что n_s = L, и переходя от dβ к ∆_β, а затем к предельным ошибкам, получим

Отсюда

а с учетом (7.14)

По формуле (7.23) можно определить влияние источника систематических ошибок на каждый отдельный угол с расчетом, чтобы общее влияние этого источника ошибок на поперечную невязку хода было в пределах, определяемых формулой (7.17).

Рассчитаем точность угловых измерений для полигонометрического хода 4 класса длиной 10 км с числом сторон п = 15. По формулам (7.21) и (7.23)

Ошибка, которая приходится на долю одного источника ошибок случайного характера, будет равна

7.8. Ошибки измерения угла

1. Вследствие неточности центрирования марок и теодолита. Необходимо измерить угол АСВ (рис. 54). Будем считать, что теодолит в точке С и марка в точке В центрированы безошибочно, марка в точке А центрирована с ошибкой. Тогда в измеряемый угол мы вносим ошибку редукции α.

Каждому положению точки А' будетсоответствовать угол α, следовательно, будет n значений угловой ошибки редукции α₁, α₂, . . . , α_n.

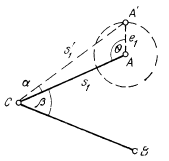
Рис. 54. Схема редукции

Средняя квадратическая ошибка редукции будет

Значение угла а определим из треугольника С А А'

о ткуда

При правильно поставленных работах угол α весьма мал и расстояния s₁ и s₁' примерно равны, поэтому можно записать

П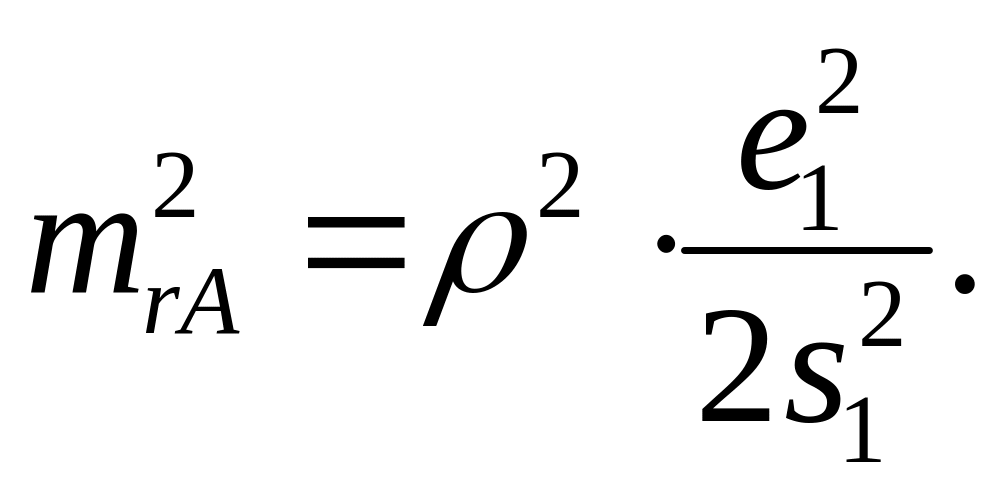 одставив в формулу (7.24) значения αi , после соответствующих преобразований получим

Аналогично можно найти выражение ошибки измерения горизонтального угла из-за неточности центрирования визирной марки в точке В

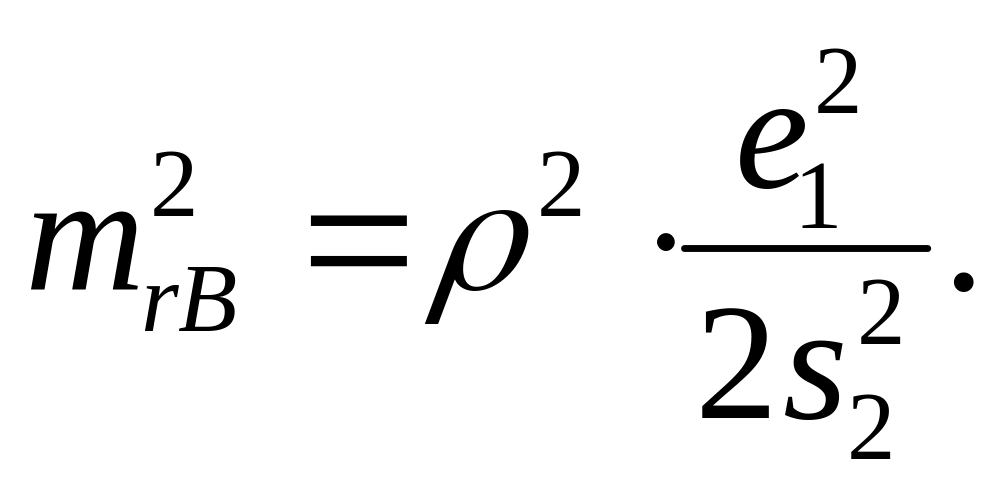
Общее влияние ошибки редукции

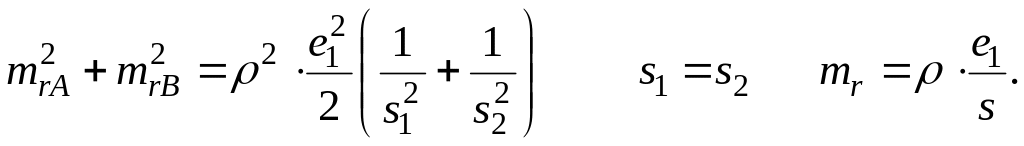
З ная величину средней квадратической ошибки, можно подсчитать величину е1 по формуле

Если принять полученную в предыдущем параграфе величину mr = 0,67", а scр = 500,0 м, то

Такую точность центрирования может обеспечить оптический центрир.

Вывод: 1) влияние ошибки редукции на ошибку измерения угла не зависит от его величины и обратно пропорционально длинам сторон, образующих угол;

2) влияние ошибки редукции тем больше, чем больше отличаются между собой длины сторон измеряемого угла.

Центрирование прибора. Предположим, что при измерении угла АСВ (рис. 55) марки в точках А и В отцентрированы безошибочно, а теодолит центриро-ван не в точке С, а в точке D.

Линейный элемент центрирования е₁, который составит со стороной СА угол Θ. Вместо угла С измеряется угол D. Проведем из точки D линии D A' и DB' , параллельные сторонам измеряемого угла С

где ∆Z - ошибка центрирования.

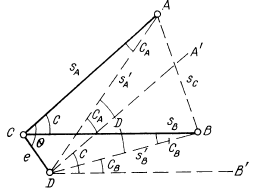
Рис. 55. Схема к центрированию инструмента

Определим значение угла СА из треугольника ACD

о ткуда

и аналогично из треугольника BCD

О кончательно будем иметь

Т ак как

В соответствии с этим формула (7.30) примет вид

При s_A = s_B = s и s_C = 2s

Из полученной формулы следует, что:

а) влияние ошибки центрирования теодолита на ошибку измерения угла зависит от его величины. Наибольшее влияние ошибка центрирования теодолита при прочих равных условиях будет оказывать при измерении углов, близких к 180°; за центрированием теодолита при угловых измерениях нужно следить очень тщательно;

б) влияние ошибки за центрирование обратно пропорционально длине сторон, образующих угол;

в) ошибка от неточного центрирования зависит от величины его линейного элемента;

г) при сравнении формул (7.27) и (7.32) видно, что m_r = m_ц .

Рис. 56. Журнал измерения углов