6.9. Критерий степени изогнутости хода

Проложить на местности ход, в котором все углы поворота равнялись бы точно 180^o, невозможно. Поэтому полигонометрический ход может считаться вытянутым лишь с некоторым приближением. Установим предел, в котором можно считать ход вытянутым, или критерий степени изогнутости полигонометрического хода, который необходим при расчетах точности ходов при их проектировании, и при оценке точности и уравнивании ходов, проложенных на местности.

В ходах вытянутой формы продольная невязка является результатом только линейных ошибок, а поперечная - только угловых.

Если ход лишь немного отклоняется по форме от прямолинейной, то влияние угловых ошибок на продольный сдвиг и линейных на поперечный будет невелико.

Получим продольную и поперечную средние квадратические ошибки и для изогнутого хода. Повернем оси координат (рис. 30) с началом в центре тяжести хода на величину дирекционного угла Θ замыкающей хода L и разложим невязку в периметре f_s на компоненты вдоль замыкающей - продольную невязку t и перпендикулярно к ней - поперечную невязку и. Обозначим координаты точек хода P_i [i = 1, 2, ..., (n + 1)] при новом положении через ξ‘_i и η‘_i , а дирекционные углы линий хода s‘_i (i = 1, 2, … , n) – через α_i

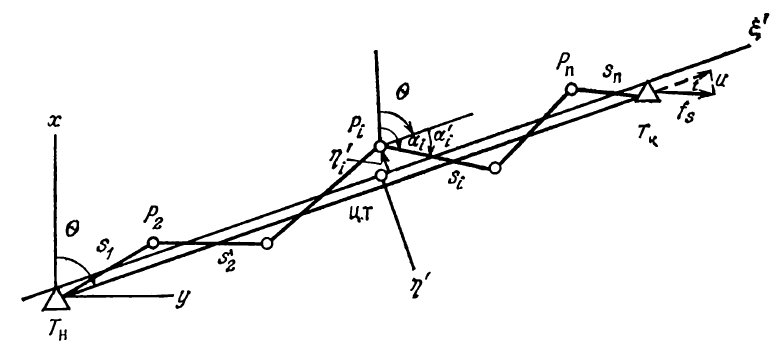
Рис. 30. Схема к определению продольной и поперечной средних квадратических ошибок

Тогда для хода с исправленными углами по аналогии c формулой (6.44) можно написать

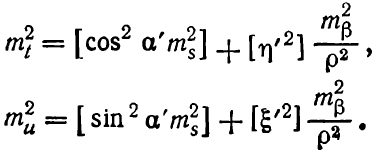
Ход можно будет считать вытянутым, если в формуле (6.71) второй, а в формуле (6.72) первый члены будут очень незначительными и могут быть отброшены, т. е.

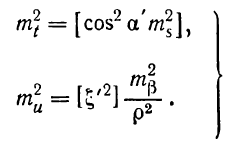
Если один из двух источников ошибок характеризуется средней квадратической ошибкой, не превышающей 1/k средней квадратической ошибки, характеризующей другой источник ошибок, то первым можно пренебречь.

На основании этого

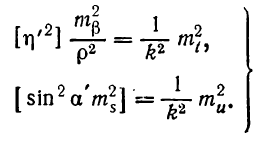
Согласно принципу равных влияний

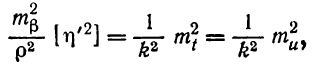
можно написать при достаточной вытянутости хода

или

Введем в выражение (6.76) среднюю величину

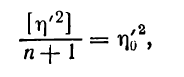
с учетом которой будем иметь

Или

Из второго уравнения (6.72) согласно принципу равных влияний напишем

При принятых равных линиях s величины mS также будут равными, поэтому в выражении (6.80) их можно вынести за знак суммы и сократить.

Введем средние величины

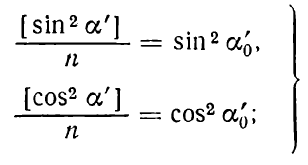
с учетом выражений (6.82) равенству (6.81) можно придать вид

О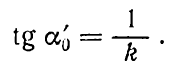 тсюда

При k = 7 для выражений (6.80) и (6.84) будем иметь

откуда α₀' ≈ 8°.

Для предельного значения согласно правилам теории ошибок находим

Следовательно, ход можно считать достаточно вытянутым, если точки хода отклоняются в обе стороны от линии, проведенной через центр тяжести параллельно замыкающей хода, в среднем на величину 1/24 (в пределе на 1/8) длины самой замыкающей и линии хода отклоняются от направления замыкающей в обе стороны на 8° (в пределе на 24°).

В качестве критерия степени изогнутости хода иногда употребляется еще отношение [s]/L. Величина дроби [s]/L будет зависеть от формы хода: чем искривленнее ход, тем эта дробь будет больше.

Ход считается достаточно вытянутым, если