6.6. Продольная и поперечная ошибки полигонометрического хода

В полигонометрическом ходе любой формы невязки f_x и f_y в приращениях координат определяют по известным формулам

Абсолютная линейная невязка f_s в периметре хода будет равна

Разложим в периметре невязку f_s на два компонента, обозначив их через t и и. Компонент t расположен вдоль хода по направлению замыкающей L, а u – перпендикулярно к ней. Продольный компонент t, который называют продольной невязкой, является следствием накопления ошибок линейных измерений, а поперечный компонент и - поперечная невязка - следствием накопления ошибок измерения углов.

Т огда

Ошибки измерения линий dL = Σds составят величину продольной невязки t = dL , средняя квадратическая величина которой согласно (6.9) будет равна

У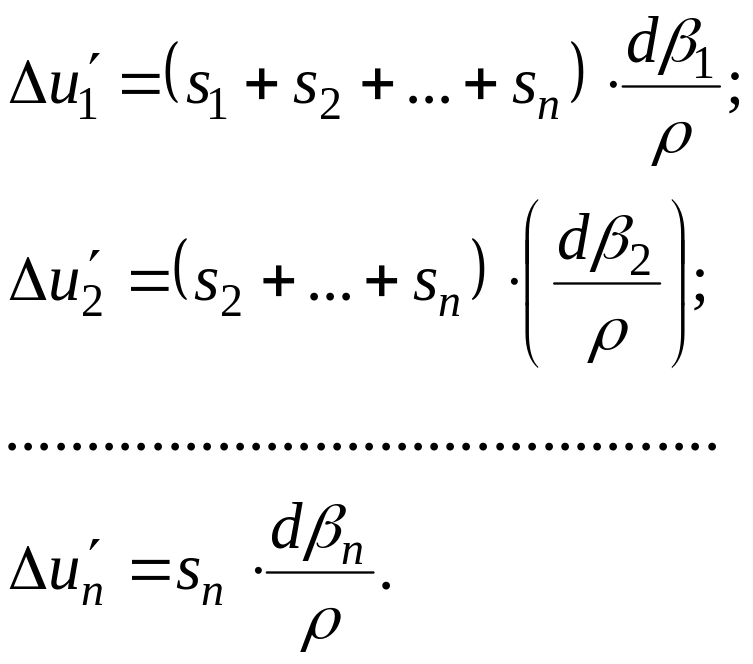 становим связь между поперечной невязкой и ошибками в углах. Если в первом угле имела место ошибка (рис. 25), то при безошибочности всех остальных углов последняя точка хода Р_n+1 переместится перпендикулярно к направлению хода на величину Δu‘₁ под влиянием ошибки dβ₂, допущенной во втором угле, точка Р_n+1 сместится на величину Δи‘₂ и т. д. и под влиянием ошибки в угле β_n смещение точки выразится через Δи‘_n. Следовательно, для смещений имеем

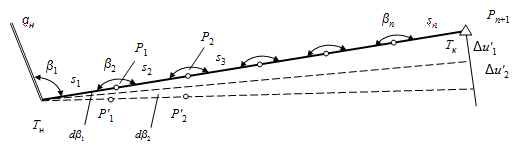
Рис. 25. Поперечная ошибка полигонометрический ход

С уммируя отдельные смещения конечной точки хода, получим поперечную невязку и'

Следовательно, с учетом (6.18), и предположив для простоты расчета, что все стороны хода примерно одинаковы, тогда

Переходя к средним квадратическим ошибкам, получим для среднего квадратического значения поперечной невязки (поперечного сдвига конечной точки хода)

Но

и мы будем иметь

Преобразуем полученное выражение. Умножим числитель и знаменатель правой части на n и положим s∙n = L, тогда формуле (6.22) можно придать вид

Или с учетом упрощений

Средняя квадратическая поперечная невязка хода зависит от длины хода, количества линий в нем и точности измерения углов.

6.7. Средняя квадратическая ошибка положения конечной точки хода

1. Ход вытянутый, углы предварительно не уравнены (рис. 24). Найдем среднюю квадратическую величину самого вектора М, которая будет называться средней квадратической ошибкой положения конечной точки полигонометрического хода,

Принимая во внимание выражения (6.17) и (6.24), будем иметь

Средняя квадратическая ошибка положения конечной точки вытянутого висячего полигонометрического хода зависит от точности измерения линий и углов в ходе, длины хода и количества линий в нем.

2. Ход изогнутый, углы предварительно не исправлены. В ходе изогнутой формы будут иметь место невязки f'_x и f'_y , и невязка в периметре выразится формулой (6.15). Предположим, что для одного и того же хода k раз измерены все углы и все линии. В соответствии с этим можно найти k значений для невязок f'_x и f'_y , а следовательно, и k значений для невязки f'_s в периметре. В результате будем иметь k равенств

где i = 1 , 2, . . . , k.

Складывая все равенства почленно и деля левую и правую части на k , получим, что каждый член равенства представляет собой соответствующее среднее квадратическое значение

С кладывая все равенства почленно и деля левую и правую части на k , получим, что каждый член равенства представляет собой соответствующее среднее квадратическое значение

Для установления связи величины М ' со средними квадратическими ошибками измерения линий m_s и углов т_β воспользуемся без вывода так называемыми координатными условными уравнениями.

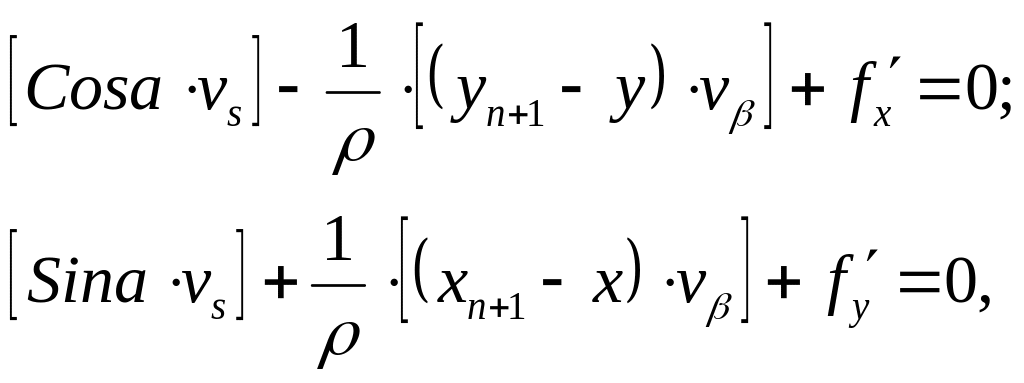
где α_i - дирекционный угол линий хода;

v_S и v_β – соответственно поправки в измеренные значения линий и углов;

х_n+1 - х и y_n+1 - y_i - разности координат между конечной и каждой точкой хода;

f'_x и f'_y - невязки в приращениях координат.

Перенесем f'_x и f'_y в правую часть в часть, и учитывая, что

м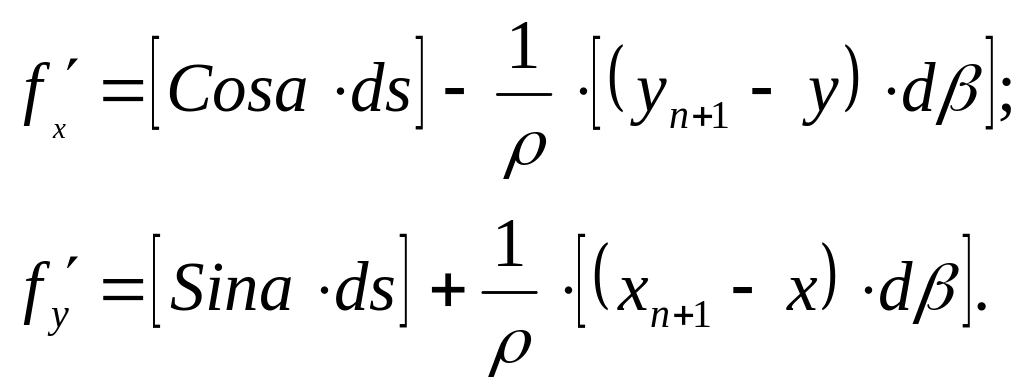 ожно записать

Переходя по правилам теории ошибок к средним квадратическим ошибкам, будем иметь

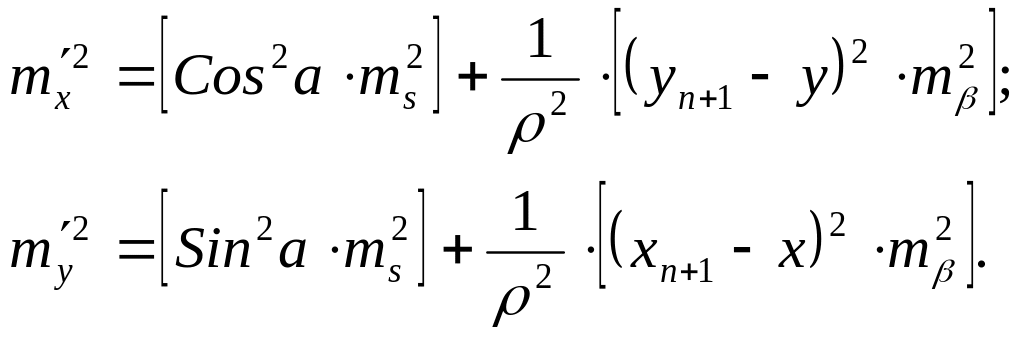
Средняя квадратическая ошибка в положении конечной точки хода М' по формуле (6.27) будет равна

Обозначим

И с учетом (6.33) можно записать

Средняя квадратическая ошибка положения конечной точки висячего изогнутого полигонометрического хода зависит не только от ошибок измерений, но и от степени изогнутости хода и количества углов поворота в нем. Величина [D²_n+1,i] будет тем меньше, чем больше изогнут ход и чем меньше в нем углов поворота.

В действительности исходные данные (координаты и дирекционные углы) сами содержат ошибки и поэтому между указанными выше величинами невязки и ошибки будет некоторая разница.

Ф ормула средней квадратической ошибки в положении конечной точки хода в этом случае будет учитывать и ошибки полевых измерений, и ошибки исходных данных

где т_αн - средняя квадратическая ошибка дирекционного угла α_н; m_(н-к) - средняя квадратическая ошибка конечного пункта Т_к по отношению к пункту Т_н .

В строго вытянутом ходе с равными сторонами дирекционные углы всех линий одинаковы и равны дирекционному углу направления всего хода α.

Для такого хода формула (6.35) преобразуется в следующий вид

3. Ход изогнутый (рис. 26), углы предварительно исправлены за невязку. Координатные условные уравнения для полигонометрического хода, в котором измеренные углы были предварительно исправлены поправками, вычисляемыми по формуле

записываются так:

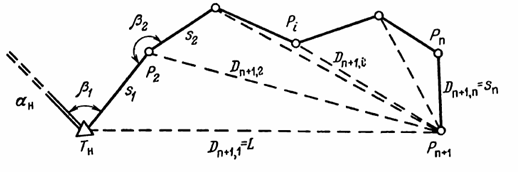
Рис. 26. Изогнутый полигонометрический ход

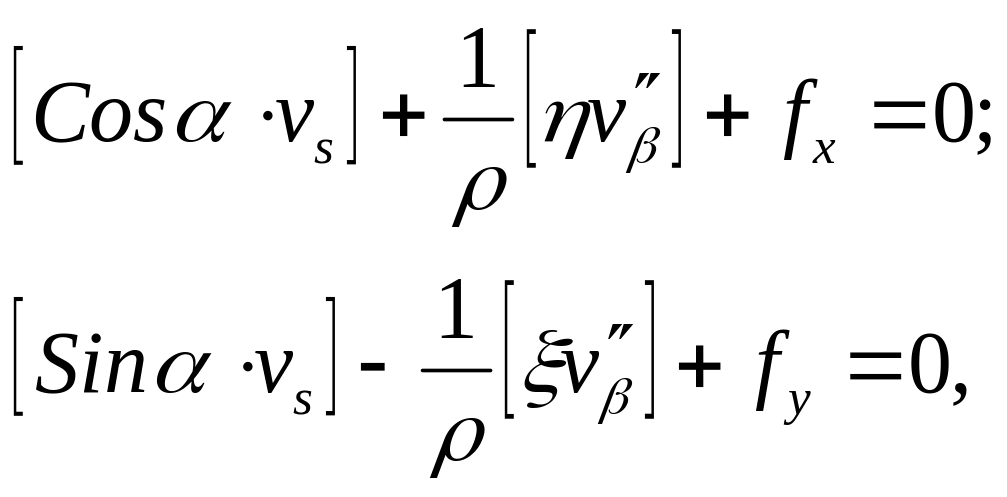
здесь η и ξ - центральные координаты (ордината и абсцисса), полученные относительно системы координат, начало которой находится в центре тяжести хода;

v" - вторичные поправки в измеренные углы.

Координаты X₀ и Y₀ центра тяжести хода определяют по формулам

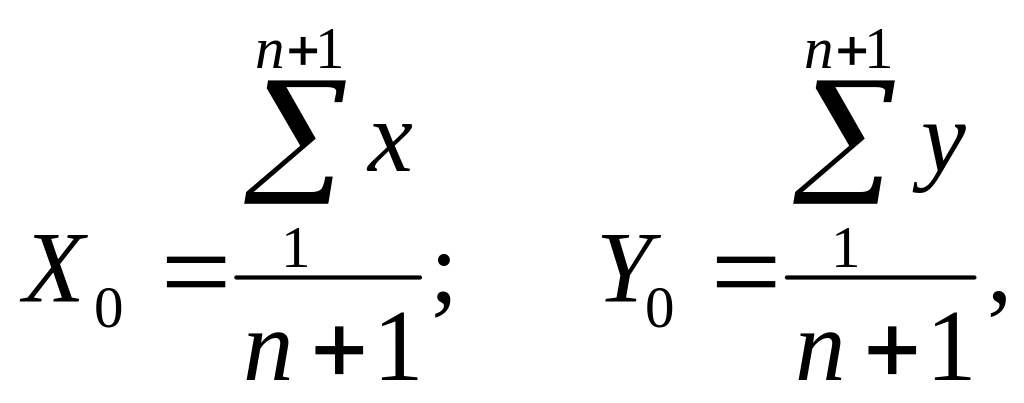
центральные координаты — по формулам

Так как η и ξ, вычисляемые по формулам (6.39), представляют собой уклонения от средних арифметических, которыми являются X0 и Y0, то, следовательно

В формулах (6.37) вторичные поправки в углы v_β" - величины зависимые, так как они входят составной частью в общие поправки в углы v_β. Следовательно, v_β" определится согласно

и подставим в (6.37). Тогда получим

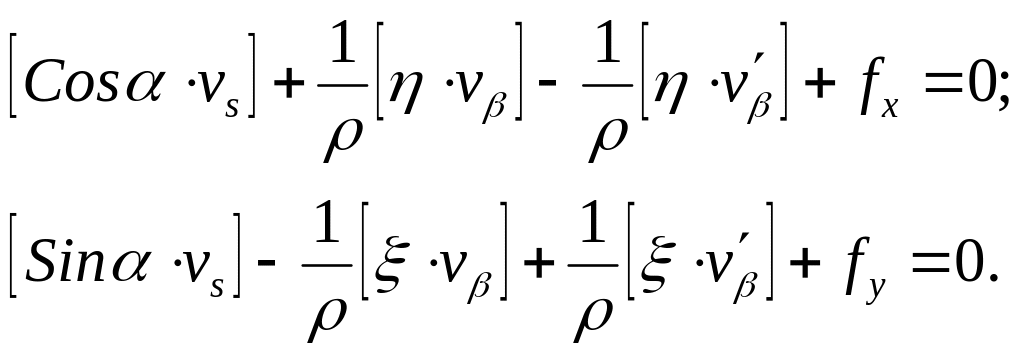
Третьи члены уравнений (6.42) будут равны нулю, так как первичная поправка v'_β - величина одинаковая для всех углов; она может быть вынесена за знак суммы, тогда суммы центральных координат по формулам (6.40) будут равны нулю.

С учетом этого уравнения (6.42) примут вид

Перенесем в уравнениях (6.43) f_x и f_y в правую часть и по аналогии с действиями в случае висячего хода заменим поправки v_s и v_β на истинные ошибки ds, dβ согласно формулам (6.29)

Переходя к средним квадратическим ошибкам (учитывая при этом, что углы в ходе измерены равноточно), будем иметь

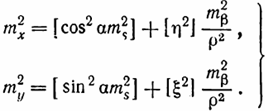
Средняя квадратическая ошибка положения конечной точки хода согласно формуле (6.27) равна сумме величин тx и ту, следовательно,

О бозначим

Здесь D₀²,_i есть расстояния между центром тяжести вершин хода и каждым его пунктом (рис. 27). С учетом (6.46) формулу (6.45) можно записать

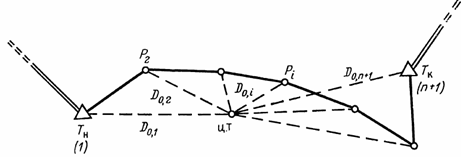
Рис. 27. Схема определения расстояний от центра тяжести до точек

т. е. средняя квадратическая ошибка положения конечной точки полигонометрического хода при исправленных за невязку углах зависит от ошибок измерений, степени изогнутости хода и количества углов поворота в нем. Величина [D²₀,i] будет тем меньше, чем меньше изломан ход и чем меньше в нем углов поворота.

Сравнивая полученную формулу с формулой (6.34), видим, что одна формула отличается от другой последним членом в правой части.

Если в исходных данных хода имели место ошибки, то формула (6.47) получит несколько иной вид; в этом случае

где D_1,0 > D_n+1,0 - соответственно расстояния от центра тяжести до начальной и конечной точек хода;

т_α - средняя квадратическая ошибка начального и конечного дирекционных углов;

m _н-к- средняя квадратическая ошибка конечного пункта Т_к по отношению к пункту T_н.

4. Ход вытянутый, углы предварительно исправлены за невязку. Положим, что вытянутый ход имеет n равных линий s, причем n - число четное, тогда центр тяжести хода будет лежать в его середине. Величину [D²₀,_i ] для такого хода можно представить выражением (рис. 28)

или

Сумма в фигурных скобках есть сумма квадратов чисел натуральног ряда, которая равна

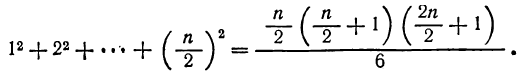
Т огда

Умножим числитель и знаменатель на n и, учитывая, что s²n² = L², получим

Разделив теперь в полученном выражении каждый член в числителе Рис. 28

и знаменателе на n и отбросив по малости величину 2/n, найдем

С учетом выражения (6.50) формула для средней квадратической ошибки положения конечной точки вытянутого полигонометрического хода будет иметь вид

При наличии ошибок в исходных дирекционных углах и координатах формула (6.51) будет иметь вид

Сравнение формул (6.36) и (6.52) показывает, что предварительное исправление углов уменьшает влияние ошибок исходных дирекционных углов на невязку в периметре в раз.

5. Ход замкнутый, углы предварительно не исправлены за невязку. Если конечная точка Тк совпадает с точкой Тн, то ход из разомкнутого превращается в замкнутый, но выведенные формулы для разомкнутого хода остаются в силе и в данном случае. Для разомкнутого хода формула (6.34) может быть представлена в виде

Как видно, при прочих равных условиях в замкнутом ходе надо ожидать среднюю квадратическую ошибку меньше, чем в соответствующем по периметру, числу углов поворота и точности угловых и линейных измерений разомкнутом ходе, особенно, если последний вытянутый.

В замкнутом ходе ошибки начального дирекционного угла и координат начального пункта не оказывают никакого влияния на величину невязки в периметре, а следовательно, и на величину М‘.

6. Ход замкнутый, углы предварительно исправлены за невязку. Формула (6.47) полностью применима и для замкнутого хода (рис. 23), только при подсчете величин [ξ²], [η²] и [D²₀,_i] точка Т_н будет участвовать дважды.

Примем приближенно замкнутый ход по форме за правильный многоугольник с равными сторонами. При n большом периметр многоугольника будет приближаться к длине окружности.

Можно положить, что D₁ ≈ R, тогда

Откуда

С ледовательно,

С учетом выражения (6.54), в котором π ≈ 10, формула (6.47) примет вид

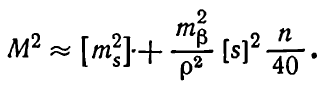
Из полученной формулы можно прийти к заключению, что и после предварительного исправления выводы, сделанные относительно величины средней квадратической ошибки замкнутого хода с углами, не исправленными за невязку, остаются в силе и в этом случае.

7. Азимутальный ход. Для полигонометрического хода любой формы с независимым определением дирекционного угла каждой линии, например из гиротеодолитных измерений, координатные условные уравнения записываются так

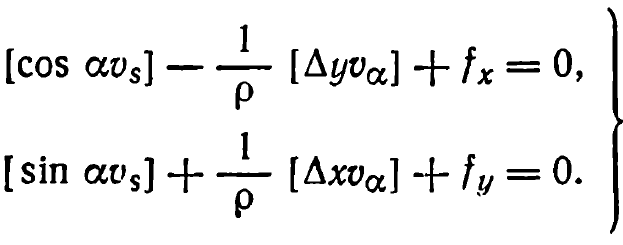
Учитывая вывод средней квадратической ошибки положения конечной точки изогнутого полигонометрического хода с измеренными углами поворота к ходу с измеренными дирекционными углами, нетрудно получить для m_x², m_y² и М² следующие выражения:

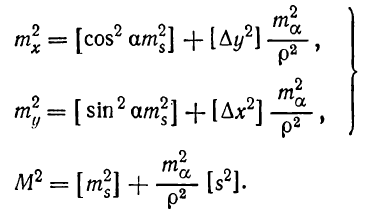
При наличии заметных ошибок в исходных координатах формула (6.58) запишется в виде

Д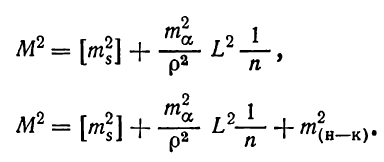 ля ходов вытянутой формы с примерно равными линиями формулы (6.58) и (6.59) примут более простой вид:

6.8. Ослабление влияния угловых и линейных ошибок

Для уменьшения влияния ошибки угловых измерений на поперечную невязку, а значит и на общий сдвиг конечной точки хода можно определить азимут, а затем и дирекционный угол некоторых линий хода путем астрономических или гиротеодолитных измерений, например Р_i , Р_n+1(рис. 29,а) или P_iN (рис. 29, б).

При этом в последнем случае одновременно измеряют примычные углы β_к1 и β_к2 для передачи дирекционного угла на стороны хода, сходящиеся в точке Pi (рис. 29, б).

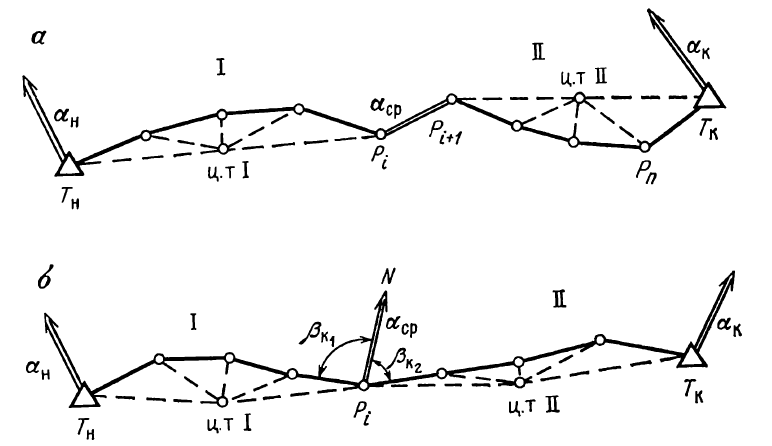
Рис. 29. Схемы к уменьшению влияния ошибок угловых

измерений на поперечный сдвиг

Наличие промежуточного дирекционного угла разбивает весь ход на две секции I и II и дает возможность вычислить невязки для каждой секции и увязать углы каждой секции отдельно. Для такого хода координатные условные уравнения записываются так:

Следовательно

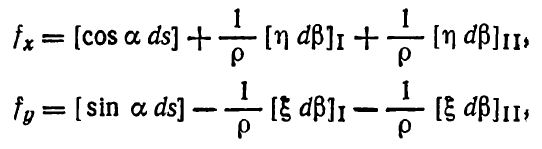
Откуда, переходя к средним квадратическим ошибкам, имеем

Суммирование квадратов ошибок дает

С учетом формулы (6.46)

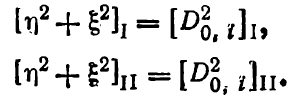
Тогда формула (6.65) примет вид:

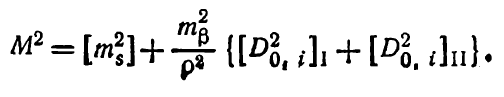
где [D₀²_,i]I , [D₀,²_i ]II - суммы квадратов расстояний от центра тяжести каждой секции до точек хода, входящих в секцию (рис. 29, а, б).

Из рис. 29 видно, что в ходе с промежуточным дирекционным углом выражение {[D₀²,_i]I+ [D₀,²_i ]II} в том же ходе без промежуточного дирекционного угла, а следовательно, будет меньше величина М - и точность хода повысится. При числе секций в ходе, равном к, выражение в фигурных скобках формулы (6.67) будет представлять сумму величин [D₀²_,i] от 1 секции до k-й.

Е сли ход будет иметь вытянутую форму и линии в ходе будут равны между собой, то

При числе линий n правую часть выражения (6.68) можно представить

Или

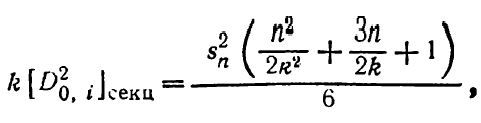
п осле преобразований

С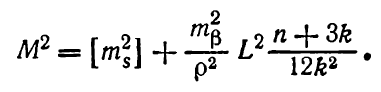 учетом (6.69) формула средней квадратической ошибки положения конечной точки вытянутого полигонометрического хода с промежуточными дирекционными углами будет иметь вид:

При числе сторон n = 16 и k = 2 при прочих равных условиях второй член в формуле (6.70) будет меньше по сравнению с формулой (6.51) в три раза. Ослабить влияние ошибок линейных измерений можно следующим образом:

1) увеличить точность измерений линий хода;

2) уменьшить длину хода между двумя исходными пунктами;

3) придать ходу прямолинейную форму.