6.4. Требования, предъявляемые к полигонометрии 4 класса, 1 и 2 разрядов

Полигонометрия 4 класса, 1 и 2 разрядов создается в виде отдельных ходов или сетей.

Полигонометрические сети должны содержать избыточное число исходных данных.

Основные показатели полигонометрии 4 класса, 1 и 2 разрядов приведены в табл. 2.

Таблица 2

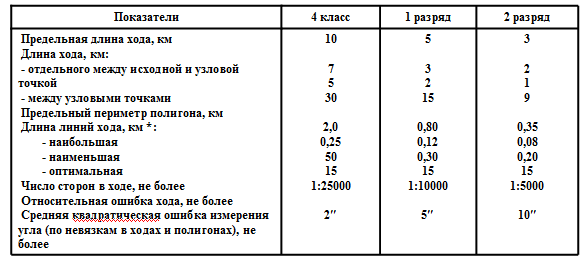
Высоты полигонометрических пунктов должны определяться нивелированием IV класса или техническим. В горной местности при обеспечении съемок с сечением рельефа через 2 и 5 м допускается определять высоты пунктов тригонометрическим нивелированием.

6.5. Действие ошибок угловых и линейных измерений

Допустим, что между двумя пунктами Pн и Pк проложен полигонометрический ход (рис. 1), в котором измерены все n сторон и все (n + 1). левых (или правых) углов. Вследствие измерения углы будут ошибочны на величины dβ₁, dβ₂, ... , dβ_(n+1) и стороны - на величины ds₁, ds₂, ... , ds_n. Исходные дирекционные углы αн, αк и исходные координаты х_н, _ун и х_к, у_к известны.

Т огда в полигонометрическом ходе измеренные значения углов вместе с исходными данными позволяют вычислить невязку в углах f_β.

Из формулы (6.1) по правилам теории ошибок получим

или, предполагая, что углы были измерены равноточно,

Так как при измерении углов имеют место источники ошибок как случайного, так и систематического характера, то каждая ошибка dβ будет состоять из случайной Δ_β и систематической σ_β частей:

dβ = Δβ + σβ,

тогда и средняя квадратическая ошибка угла β согласно теории ошибок будет также включать в себя систематическую и случайную части:

Если считать, что дирекционные углы α_н, α_к также имеют ошибки, то по (6.1) с учетом выражения (6.2) можно найти

От средней квадратической ошибки суммы углов по формуле (6.2) перейдем к предельной, которая является ни чем иным, как невязкой

пред f_β = пред dβ

П олагая, что пред dβ = 2т_β, запишем

пред f_β = пред 2т_β

Линейная ошибка хода. Для простоты рассуждений положим, что полигонометрический ход имеет вытянутую форму (рис. 24). Для такого хода можно написать

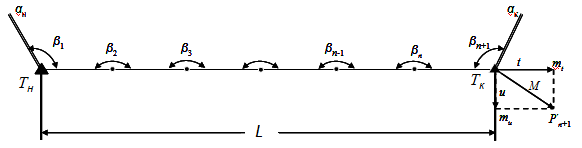
Рис. 24. Вытянутый ход полигонометрии

L = S ₁+ S₂ + …+ S_n = [S],

где L - расстояние между крайними пунктами Т_н и Т_к - замыкающая хода.

Ошибка измерения всех линий dL в вытянутом ходе в результате ошибок, допущенных в каждой линии ds_i согласно (6.7) будет

dL = ds₁ + ds₂ + … + ds_n.

Переходя к средним квадратическим ошибкам, получим

Так как при измерении линии действуют источники ошибок случайного и систематического характера и ошибка каждой линии ds_i состоит из случайной Δ и систематической σ частей

ds_i = Δ_si + σ_si ,

г де i = 1, 2, ..., n, то

Структура величин m_Δ и т_σ будет зависеть от метода измерения линий. При измерении линий, например, светодальномером и инварной проволокой она будет совершенно разной.

Е сли при измерении линий отсутствуют систематические ошибки, т. е. σ_si = 0, то

Систематическим влиянием можно пренебречь и в том случае, если средняя квадратическая систематическая ошибка по своей величине не превышает 1/3 средней квадратической случайной ошибки. Действительно, если принять

то

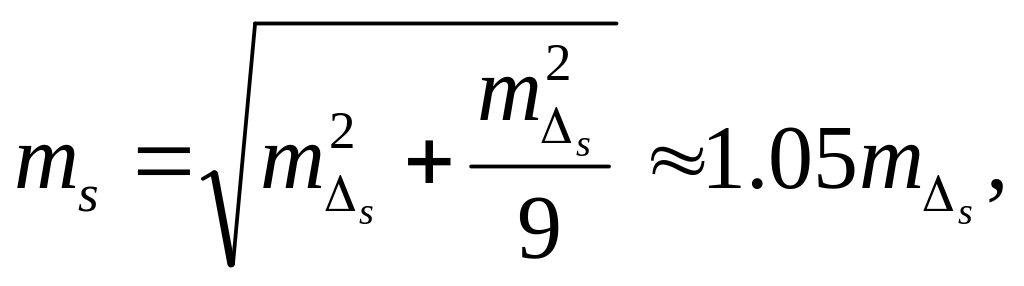
т. е. значение m_s, если пренебречь систематической ошибкой, уменьшится на 5%. При

значение ms уменьшится на 2%, следовательно, в этом случае также можно считать, что