5.2.5. Понятие о системе линейно-угловых ходов

Совокупность линейно-угловых ходов, имеющих общие точки, называют системой ходов; узловой точкой называется точка, в которой сходятся не менее трех ходов. Как и для отдельного линейно - углового хода, для системы ходов применяют строгую и упрощенную обработку измерений. Упрощенную обработку рассмотрим на примере системы из трех линейно-угловых ходов с одной узловой точкой (рис. 21). Каждый ход опирается на исходный пункт с известными координатами; на каждом исходном пункте имеется направление с известным дирекционным углом.

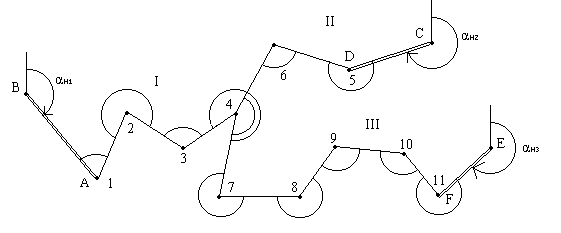
Рис. 21. Система линейно-угловых ходов с одной узловой точкой

Одну сторону какого-либо хода, проходящую через узловую точку, принимают за узловое направление (4-7) и вычисляют ее дирекционный угол по каждому ходу в отдельности, начиная от начального дирекционного угла в ходе. Получают три значения дирекционного угла узлового направления:

α₁ - из первого хода, α₂ - из второго хода, α₃ - из третьего хода,

и вычисляют средневесовое значение из трех, причем за вес отдельного значения принимают число 1/n_i , где n_i - количество углов в ходе от исходного направления до узлового направления (на рис. 21 n₁ = 4, n₂ = 3, n₃ = 5):

Считая узловое направление исходным, т.е. имеющим известный дирекционный угол, вычисляют угловые невязки в каждом ходе по отдельности и вводят поправки в измеренные углы.

По приращениям координат вычисляют координаты узловой точки по каждому ходу в отдельности и получают три значения координаты X и три значения координаты Y узловой точки. Средневесовые значения координат подсчитывают по формулам:

Считая узловую точку исходным пунктом с известными координатами, вычисляют координатные невязки для каждого хода в отдельности и вводят поправки в приращения координат по сторонам ходов. По исправленным приращениям координат вычисляют координаты пунктов всех ходов.

Упрощенная обработка системы линейно - угловых ходов с одной узловой точкой состоит из двух этапов: получение дирекционного угла узлового направления и координат узловой точки и обработка каждого хода в отдельности.

6. Полигонометрия 6.1. Принцип построения государственной геодезической сети

При создании ГГС возникают три вопроса, имеющие принципиальное значение:

- выбор схемы построения государственной геодезической сети на всей территории страны;

- установление плотности геодезических пунктов;

- установление точности определения взаимного положения смежных пунктов в сети.

Каждый из этих вопросов необходимо рассматривать совместно, причем с двух точек зрения:

- решения основных научных задач геодезии;

- решения задач картографирования территории страны.

ГГС создают поэтапно, соблюдая принцип перехода от общего к частному.

Сначала строят главную, состоящую из крупных геодезических построений в виде либо замкнутых полигонов. Измерения выполняют с наивысшей точностью.

Затем данную сеть принимают за исходную и строят геодезическую сеть второго порядка с более детальными геометрическими построениями и с меньшей относительной точностью измерений. С теми же величинами абсолютных ошибок определения взаимного положения смежных пунктов, как и в сети первого порядка.