4. Плановые сети сгущения
4.1. Постановка задачи
Задача сгущения существующей геодезической сети возникает постоянно при реализации на практике принятого в нашей стране принципа построения геодезических сетей “от общего к частному”. Сгустить сеть – это значит, что к существующим пунктам геодезических сетей высокого класса точности требуется добавить ещё один или несколько пунктов более низкого класса точности так, чтобы плотность пунктов оказалась соответствующей требованиям проводимых работ.
Можно предложить несколько вариантов определения координат точек в одном геодезическом построении. Из этого множества вариантов выделились и оформились в виде самостоятельных способов, для которых была разработана соответствующая теория, следующие:
- геодезические засечки;
линейно-угловой ход;
система линейно-угловых ходов с узловыми точками;
триангуляция;
трилатерация;
линейно-угловая сеть.
Геодезические засечки применяют тогда, когда нужно определить прямоугольные координаты одной точки; такая задача возникает при привязке свободных или висячих геодезических построений к исходным пунктам, а также при сгущении геодезической сети на малом по территории участке местности, либо когда существует довольно густая сеть исходных пунктов и только в отдельных местах требуется расположить дополнительно по одному – два пункта сгущения.
Остальные способы предназначены для определения координат нескольких пунктов из одного геодезического построения.
4.2. Определение прямоугольных координат одной точки
4.2.1. Способы задания прямоугольной системы координат
Как известно, система прямоугольных координат на плоскости может задаваться тремя способами:
1-й способ - стандартный математический:
фиксируется местоположение центра системы точки 0, проводится ось 0X и указывается ее положительное направление;
- перпендикулярно к оси 0X проводится ось 0Y, в соответствии с типом системы (правая или левая) указывается положительное направление оси 0Y;
устанавливается масштаб координат вдоль осей.
При наличии координатных осей для определения координат какой-либо точки C нужно сначала опустить перпендикуляры из этой точки на координатные оси и затем измерить длину этих перпендикуляров; длина перпендикуляра к оси 0X равна координате Y, длина перпендикуляра к оси 0Y - координате X точки (рис.24 ).
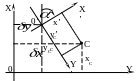
Рисунок 24 – Прямоугольная система координат
Кроме
системы XOY
можно
использовать систему X’0’Y’,
получающуюся из системы X0Y
путем
параллельного переноса начала координат
в точку 0’
(
),
и
поворота осей координат по часовой
стрелке на угол .
Переход из системы X0Y
в систему X’0’Y’
выполняется
по формулам
,
.
Для обратного перехода используются формулы
,
.
В
частном случае угол
может быть равен нулю.
2-й способ - координатная сетка:
- проводятся две взаимно перпендикулярные системы параллельных линий; расстояния между линиями одинаковые;
считается, что эти линии параллельны осям координат, и у каждой линии подписывается значение соответствующей координаты.
Все действия по определению координат точки или по нанесению точки по её известным координатам выполняются внутри соответствующего квадрата, юго-западный угол которого принимается за начало местной системы координат, имеющей силу только внутри данного квадрата.
3-й способ - указываются численные значения координат двух фиксированных точек.
Первый способ является общепринятым; в геодезии этим способом задается зональная система координат Гаусса.
На топографических картах и планах система прямоугольных координат Гаусса задается вторым способом.
На местности система прямоугольных координат задается третьим способом; всегда можно найти несколько геодезических пунктов с известными координатами и определять координаты точки или выносить точку на местность по её известным координатам относительно этих пунктов, выполняя какие-либо измерения.