1.Понятие о форме и размерах Земли.Геоид и референц — эллипсоид Красовского.

Первоначальное представление о фигуре З. – шар (Пифагор). З., вращаясь вокруг оси, имеет сжатие, форму, близкую к эллипсоиду. Ур-ная пов-сть – выпуклая линия, в каждой точке к-рой направление силы тяж. перпенд-но к этой ур-ной пов-сти (напр-е силы тяж. – отвесная линия).

Пов-сть Геоида – ур-ная пов-сть, совпадающая с пов-стью морей и океанов в спокойном их состоянии и мысленно продолженная под материками.

Земной эллипсоид – элл., харак-щий форму и размеры З. вообще.

Референц-элл. – земной элл., к-рый принят для обработки геод. изм. и уст-я системы геод. координат (реф.-элл. Красовского) (а=6 378 245 м, α=(а-b)/а=1/298,3, b= 6 356 863 м, где а и b - большая и малая полуоси элл., α – полярное сжатие.

За фигуру Земли принимают геоид. Геоид – фигура ограниченная уровневой поверхностью совпадающей с поверхностью Мирового океана в состоянии полного покоя и мысленно продолженной под материками. Поверхность геоида отличается от физической поверхности Земли. Поверхность геоида в каждой ее точке перпендикулярна направлению отвесной линии.

Геоид сложная фигура, поэтому перешли от него к поверхности эллипсоида вращения.  R-земли - ~6371 км, 1 градус на экваторе = 111 км, 1’=1 морской миле 18 км.

Поверхность Земли общей площадью 510 млн км2 имеет возвышения и углубления, заполненные водой. Поверхность морей и океанов занимает 71 %, а суша всего лишь 29 % от общей поверхности Земли. Поэтому за фигуру Земли принимают поверхность воды океанов в спокойном состоянии, мысленно продолженную под материками. Такая поверхность называется уровенной поверхностью Земли. Уровснная поверхность в любой точке перпендикулярна к отвесной линии, проходящей через эту точку. Уровенная поверхность Земли имеет сложную форму и называется поверхностью геоида, а тело, ограниченное ею, — геоидом. Исследованиями установлено, что фигура геоида близко подходит к поверхности сфероида С ф е р о и д о м называется эллипсоид, который получается от вращения эллипса вокруг его малой оси. Размеры земного эллипсоида определяются длинами большой и малой полуосей (рис. 1): а — большая полуось или радиус экватора;

b — малая полуось или полуось вращения Земли. Величина

а = (а — b)/а называется сжатием земного эллипсоида. Величины а и b определяются посредством градусных измерений в различных местах меридиана. В разное время ученые многих стран занимались определением размеров Земли. Наиболее точные результаты получили Ф. Н. Красовский и А. А. Изотов в 1940 г. Размеры земного эллипсоида, получившего название ≪эллипсоид Красовского≫, приняты для геодезических и картографических работ на всей территории нашей страны (а = 6 378 245 м; Ъ = 6 356 863 м; а = 1 : 298,3).

Уровенная поверхность Земли в одних местах возвышается, в

других понижается над поверхностью эллипсоида. Однако отклонение не превышает 150 м.

Для решения многих задач прикладного значения Землю можно принимать за шар. Радиус такого шара, равного по объему земному эллипсоиду, по вычислениям Ф. Н. Красовского равен 6371,11 км.

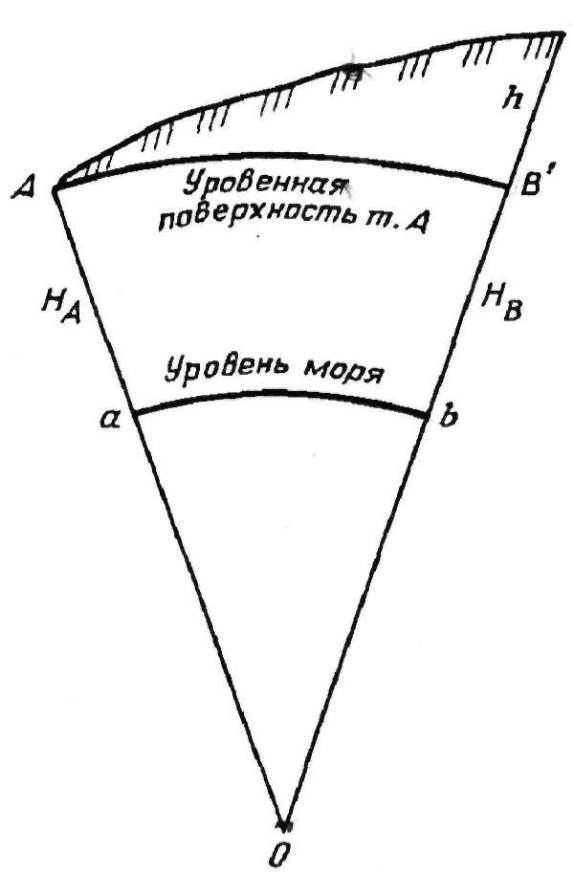
2. Абсолютные и относительные высоты точек земной поверхности. Балтийская ситема высот. Абсолютной высотой точки земной поверхности называется расстояние от этой точки по отвесной линии до уровeнной поверхности, принятой за начало счета. Числовое значение высоты называется отметкой. В России счет абсолютных высот ведется от среднего уровня Балтийского моря, от нуля Кронштадтского футштока. Если расстояние от точки земной поверхности берется не до уровенной поверхности моря, а до какой-нибудь другой условной поверхности, то и отметка называется условной. Величины Аа = НА и Вb = Нв (рис. 5) есть абсолютные высоты точек А и В земной поверхности. Расстояние от точки земной поверхности по отвесной линии до уровенной поверхности, проведенной через другую точку, называется относительной высотой или превышением

одной точки над другой. Величина h есть превышение

точки В над точкой А. Превышение может иметь знак плюс или

минус в зависимости от положения определяемой точки. Если

определяемая точка находится выше по отношению к другой, то

превышение положительное, а если ниже, то отрицательное.