2.Тройные интегралы

Пусть VR³ – замкнутая область, ограниченная непрерывной поверхностью. Пусть f(x,y,z) – функция, заданная и ограниченная на V. Пусть V = V₁V₂ … V_n, где V_1, V₂, … V_n – области, не имеющие общих внутренних точек. Обозначим через v_k объем области V_k, а через d_k – ее диаметр. Пусть d = – диаметр разбиения V_1, V₂, … V_n. В каждой области V_k выберем точку ( ,_k) и составим интегральную сумму, соответствующую данному разбиению: S = .

Определение. Если существует предел интегральных сумм при d0, не зависящий от разбиения, то функция f(x,y,z) называется интегрируемой в области V, а предел интегральных сумм называется тройным интегралом функции f(x,y,z) по области V и обозначается .

1^о. Если функция f(x,y,z) непрерывна в области V, то она интегрируема в этой области.

2^о. Пусть область V заполняет неоднородное тело, точечная плотность которого в точке (x,y,z) равна (x,y,z). Тогда масса этого тела равна (физический смысл тройного интеграла).

Все свойства тройного интеграла повторяют свойства двойного: аддитивность, линейность, неравенства, теорема о среднем. При этом равен объему области V (геометрический смысл тройного интеграла).

Пусть область V ограничена гладкими поверхностями z=(x,y) и z=(x,y), где (x,y)D (проекция области V на плоскость x0y), причем (x,y)(x,y) при (x,y)D. Тогда = , то есть вычисление тройного интеграла сводится к вычислению двойного и одинарного.

Пример. 1) Вычислим , где область V ограничена параболоидом z=x²+y² и плоскостью z=1. Проекция D этой области на плоскость х0у – круг x²+y²1. Поэтому = 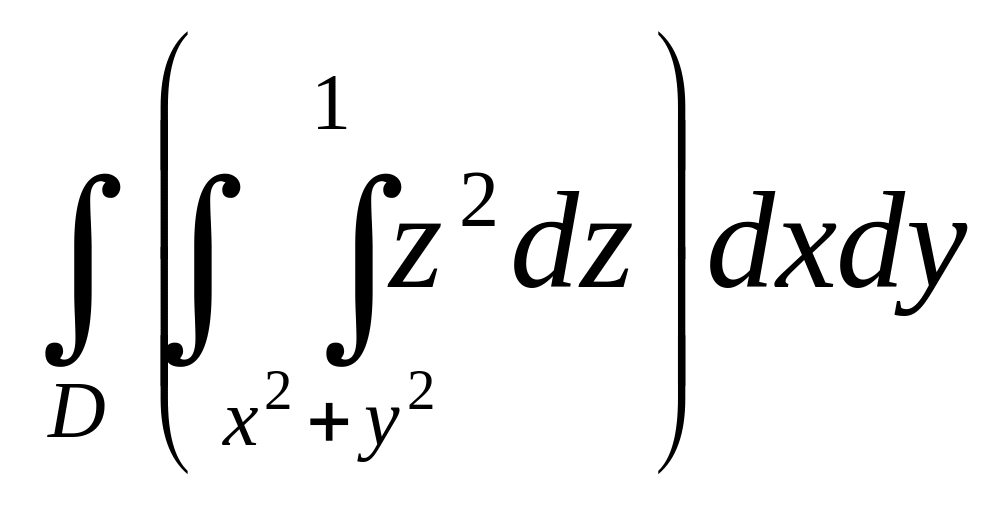= = = . Перейдем к полярным координатам: = = = = = .

2) Вычислим , где V – тетраэдр, ограниченный координатными плоскостями и плоскостью 2х+2у+z–6 = 0. Проекция D этого тетраэдра на плоскость х0у – треугольник ОАВ, где О – начало координат; уравнение прямой АВ: х+у–3=0, А(3;0;0), В(0;3;0). Поэтому = = = = = = = = = .

3.Криволинейные интегралы

3.1.Криволинейный интеграл I рода

Пусть функция f(x,y) определена и непрерывна во всех точках гладкой дуги L=AB, заданной уравнением y=(x), где axb. Рассмотрим разбиение этой дуги точками А₀, А₁, …, А_n, где А₀ = А, А_n = В. Пусть s_k – длина дуги A_k-1A_k, d= – диаметр разбиения. Выберем на каждой дуге A_k-1A_k точку (_k,_k). Сумма s_k называется интегральной суммой I рода.

Определение. Если существует предел интегральных сумм I рода при d0, не зависящий от разбиения, то этот предел называется криволинейным интегралом I рода функции f(x,y) по дуге L и обозначается .

Можно доказать, что криволинейный интеграл I рода равен определенному интегралу . Если же кривая L задана параметрически уравнениями x=x(t), y=y(t), t, то криволинейный интеграл I рода равен .

Если дуга L имеет линейную плотность f(x,y)>0, то масса этой дуги равна (физический смысл криволинейного интеграла I рода).

Примем без доказательства свойства аддитивности и линейности криволинейного интеграла I рода.

1^о. Если дуга L является объединением дуг L₁ и L₂, имеющих не более одной общей точки, и существуют и , то существует и , равный их сумме.

2^о. = + .

3^о. =  .

Важным свойством криволинейного интеграла I рода является его независимость от направления интегрирования:

4^о. = .