6.2.Длина гладкой дуги

Пусть дуга представляет собой часть графика функции у=f(x), имеющей на отрезке [a;b] непрерывную производную. Такая дуга называется гладкой. Ее длину можно найти по формуле: L= .

Пример. Найдем длину части цепной линии y=chx при 0x1.L= = =shx =sh1 =0,5(e–e^–1).

Пусть дуга задана параметрически: х=х(t), у=y(t), где t[a;b], – причем функции х(t) и y(t) имеют на отрезке [a;b] непрерывные производные. Тогда длину дуги можно найти по формуле: L= .

Пример. Найдем длину части астроиды x=cos³t, y=sin³t при 0t . L= =

= = =

= = = =1,5.

Пусть дуга задана в полярных координатах: =(), [;], – причем функция () имеет на отрезке [;] непрерывную производную. Тогда длину дуги можно найти по формуле: L= .

Пример. Найдем длину части окружности =2cos при 0 . L= = = .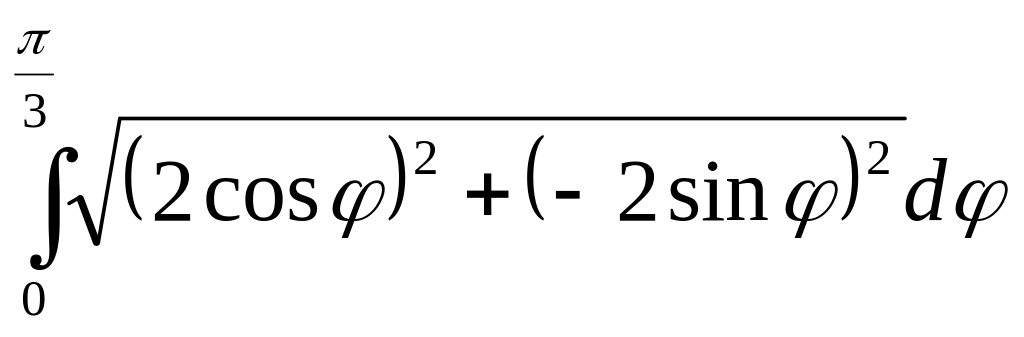

6.3.Объем тела

Рассмотрим тело, заключенное между плоскостями х=а и х=b (a<b). Пусть S(x) – площадь его сечения плоскостью, проходящей через точку х оси абсцисс перпендикулярно этой оси, причем функция S(x) непрерывна на отрезке [а;b]. Тогда объем тела можно найти по формуле: V= .

В частности, для тела, полученного вращением криволинейной трапеции, ограниченной линиями x=a, x=b, y=f(x), y=0 (a<b, f(x)0), около оси абсцисс, каждое сечение – круг радиуса f(x). Значит, площадь сечения равна (f(x))² и формула объема тела вращения: V= .

Примеры. 1) Рассмотрим пирамиду, высота которой представляет собой отрезок оси абсцисс от 0 до H, а основание лежит в плоскости yOz и имеет площадь S. Тогда площадь S(x) сечения, проходящего через точку х оси абсцисс перпендикулярно этой оси, равна S . Находим объем пирамиды: V= =

= = .

2) Рассмотрим шар с центром в начале координат и радиусом R. Он представляет собой тело, полученное вращением полукруга, ограниченного линиями x=–R, x=R, y=0, y= , около оси абсцисс. По формуле объема тела вращения V= = = .

3) Рассмотрим конус, высота которого представляет собой отрезок оси абсцисс от 0 до H, а основание лежит в плоскости yOz и имеет радиус R. Он представляет собой тело, полученное вращением треугольника, ограниченного линиями x=0, x=H, y=0, y= (H–x), около оси абсцисс. По формуле объема тела вращения V= =

= = .

6.4.Центр масс и моменты инерции

1. Координаты центра масс гладкой однородной дуги, заданной уравнением y=f(x), axb, можно найти по формулам: х_о= , у_о= .

Координаты центра масс однородной пластины, ограниченной линиями x=a, x=b, y=f(x), y=0 (a<b, f(x)0), можно найти по формулам: х_о= , у_о= .

Примеры. 1) Найдем координаты центра масс однородной дуги цепной линии: y=chx, –1x1.

х_о= = =xshx – =sh1–sh1–ch1 +ch1=0. у_о= = = =

= =1+0,5sh2.

2) Найдем координаты центра масс однородной пластины, представляющей собой часть эллипса x=4cost, y=3sint, лежащую в первой четверти.

х_о= = = .

у_о= = = .

2. Величину моментов инерции относительно осей Ох и Оу для гладкой однородной дуги, заданной уравнением y=f(x), axb, можно найти соответственно по формулам:

I_х = , I_у = .

Величину моментов инерции относительно осей Ох и Оу для однородной пластины, ограниченной линиями x=a, x=b, y=f(x), y=0 (a<b, f(x)0), можно найти соответственно по формулам: I_х = , I_у = .

Примеры. 1) Найдем момент инерции I_х для однородной полуокружности: y= , –1x1.

I_х= = = = .

2) Найдем момент инерции I_у для однородной пластины, ограниченной эллипсом x=4cost, y=3sint.

I_у = = = =

= =48.