20. Деформации твердого тела. Закон Гука.

Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругоемеханическое напряжение.

Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия(другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).

Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.

Виды деформации 

Диаграмма, показывающая зависимость между механическим напряжением (σ) и деформацией (ε) обобщённого материала. Слева — упругие деформации, справа — пластические

Наиболее простые виды деформации тела в целом: растяжение-сжатие, сдвиг, изгиб, кручение.

В большинстве практических случаев наблюдаемая деформация представляет собой совмещение нескольких одновременных простых деформаций. В конечном счёте, однако, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.

Изучение деформации. Деформация физического тела вполне определяется, если известен вектор перемещения каждой его точки.

Деформация твёрдых тел в связи со структурными особенностями последних изучается физикой твёрдого тела, а движения и напряжения в деформируемых твёрдых телах — теорией упругости и пластичности. У жидкостей и газов, частицы которых легкоподвижны, исследование деформации заменяется изучением мгновенного распределения скоростей.

Причины возникновения деформации твёрдых тел. Деформация твёрдого тела может явиться следствием фазовых превращений, связанных с изменением объёма, теплового расширения, намагничивания (магнитострикция), появления электрического заряда (пьезоэлектрический эффект) или же результатом действия внешних сил.

Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke)^[1]. Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь   — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а   — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения   и длины  ) явно, записав коэффициент упругости как

Величина   называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение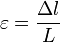

и нормальное напряжение в поперечном сечении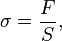

то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Обобщённый закон Гука

В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга   и содержит 81 коэффициент. Вследствие симметрии тензора  , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

где   — тензор напряжений,   — тензор деформаций. Для изотропного материала тензор   содержит только два независимых коэффициента.