14. Удар (упругий и неупругий).

Удар – это столкновение 2 или более тел, при котором взаимодействие длится очень короткое время.

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется.

Для такого удара выполняются  закон сохранения энергии и закон сохранения импульса.

Абсолютно неупругий удар – удар, в результате которого тела объединяются и двигаются дальше как едино целое.

(15-16)15. Момент инерции и теорема Штейнера.

Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадрат их расстояния до рассматриваемой оси.

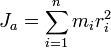
Теорема Гюйгенса-Штейнера: Момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллелтной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями.

1 6. Кинетическая энергия вращения.

Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m₁, m₂,..., m_n , находящиеся на расстоянии r₁, r₂,..., r_n от оси. 

При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами m_i опишет окружность соответствующих радиусов r_i; при этом объем будет иметь соответствующую линейную скорость v_i. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:   (1) 

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:    

Используя выражение (1), получаем   

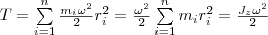
где J_z - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела 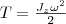  (2) 

Из сравнения формулы (2) с выражением для кинетической энергии поступательно движущегося тела (T=mv²/2), мы видим, что момент инерции является мерой инертности тела при вращательном движении. Формула (2) справедлива для тела вращающегося вокруг неподвижной оси. 

В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:   

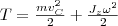
где m - масса катящегося тела; v_c - скорость центра масс тела; J_c - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

17. Момент силы и основное уравнение динамики вращательного движения твердого тела.

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точ­ки О в точку Априложения силы, на силу F (рис. 25):

Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы

                                                        (18.1)

где — угол между r и F; r sin = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина M_z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента М_z не зависит от выбора положения точки О на оси z.

Е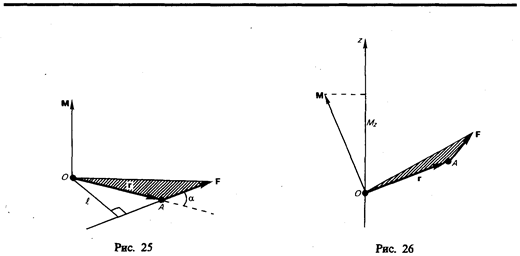 сли ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

Найдем выражение для работы при вращении тела (рис. 27). Пусть сила F приложе­на в точке В, находящейся от оси z на расстоянии r,  — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d точка приложения В проходит путь ds=rd и работа равна произведе­нию проекции силы на направление смещения на величину смещения:

                                                                    (18.2)

Учитывая (18.1), можем записать

где Frsin  = Fl =M_z — момент силы относительно оси z. Таким образом, работа при вращении тела  равна произведению момента действующей силы на угол поворота.

Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но 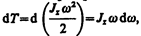  поэтому M_zd = J_zd, или

Учитывая, что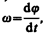  получаем 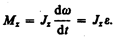                    (18.3)

Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Можно показать, что если ось z совпадает с главной осью инерции (см. § 20), проходящей через центр масс, то имеет место векторное равенство                                     (18.4)

где J — главный момент инерции тела (момент инерции относительно главной оси).

(18-20)18. Момент импульса и закон его сохранения.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произ­ведением:

где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс мате­риальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Модуль вектора момента импульса

где  — угол между векторами r и р, l — плечо вектора р относительно точки О.

М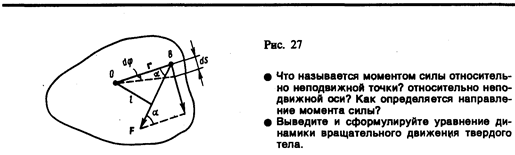 оментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдель­ная точка тела движется по окружности постоянного радиуса r_i с некоторой скоро­стью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. с. радиус является плечом вектора m_iv_i . Поэтому можем записать, что момент импульса отдель­ной частицы равен

                                                                (19.1)

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

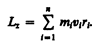
Для замкнутой системы тел, не взаимодействующих с другими телами, не включенными в систему, момент внешних сил равен нулю, поэтому для замкнутой системы суммарный момент импульса сохраняется. Это утверждение выражает еще один фундаментальный физический закон − закон сохранения момента импульса.