12. Кинетическая и потенциальная энергия.

Кинетическая энергия механической системы - это энергия механического движения рассматриваемой системы. 

Сила F, воздействуя на покоящееся тело и приводя его в движение, совершает работу, а энергия движущегося тела увеличивается на величину затраченной работы. Значит, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, тратится на увеличение кинетической энергии dT тела, т. е.    Используя второй закон Ньютона   и умножая на перемещение dr получаем 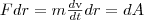   Так как v=dr/dt, то dA=mvdv,

откуда   

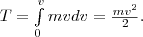
Таким образом, тело массой m, движущееся со скоростью v, обладает кинетической энергией   (1) 

Из формулы (1) видно, что кинетическая энергия зависит только от массы и скорости тела (или точки), т. е. кинетическая энергия тела зависит только от состояния ее движения. 

При выводе формулы (1) по умолчанию предполагалось, что движение рассматривается в инерциальной системе отсчета, в противном случае нельзя было бы использовать законы Ньютона. В различных инерциальных системах отсчета, движущихся относительно друг друга, скорость тела (точки), а следовательно, и его кинетическая энергия будут отличаться. Значит, кинетическая энергия зависит от выбора системы отсчета. 

Потенциальная энергия - механическая энергия системы тел, которая определяется характером сил взаимодействия между ними и их взаимным расположением. 

Пусть взаимодействие тел друг на друга осуществляется силовыми полями (например, поля упругих сил, поля гравитационных сил), которые характеризуются тем, что работа, совершаемая действующими в системе силами при перемещении тела из первое положения во второе, не зависит от траектории, по которой это перемещение произошло, а зависит только от начального и конечного положений системы. Такие поля называются потенциальными, а силы, действующие в них, - консервативными. В случае, если работа силы зависит от траектории перемещения тела из одного положения в другое, то такая сила называется диссипативной; примером диссипативной силы является сила трения. 

Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией P. Работа консервативных сил при элементарном (бесконечно малом) изменении состоянии системы равна приращению потенциальной энергии, взятому с отрицательным знаком, так как работа производится за счет уменьшения потенциальной энергии:   (2) 

Работа dA выражается как скалярное произведение силы F на перемещение dr и выражение (2) примет вид  (3) 

Значит, если известна функция P(r), то из (3) можно найти силу F по модулю и направлению.  Потенциальная энергия может быть найдена, используя (3) как   

(13-14)13. Закон сохранения механической энергии.

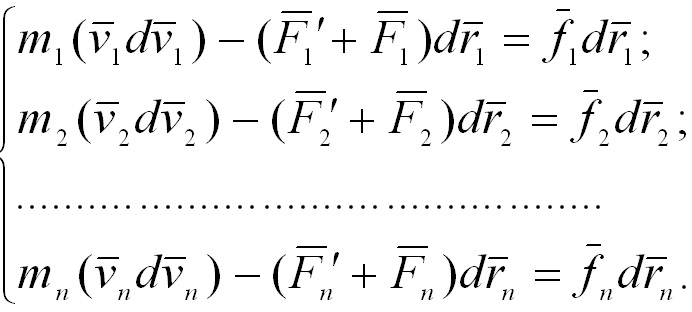
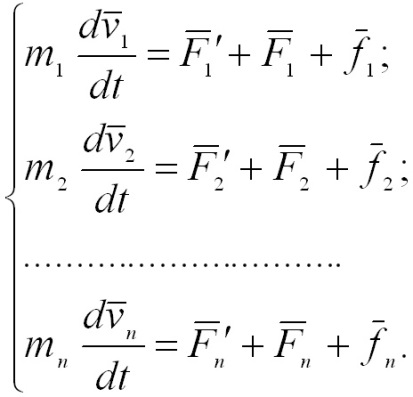Учитывая, что  , получим:

    

  Складывая эти уравнения, получим: (3.13) 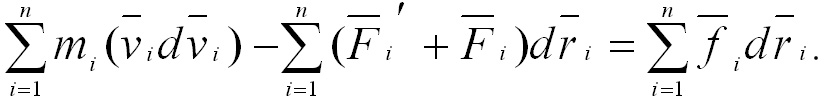            Первый член левой части (3.13) представляет собой приращение кинетической энергии системы:

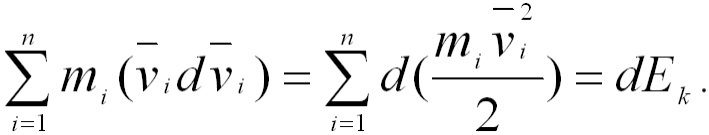      Второй член   равен элементарной работе внутренних и внешних консервативных сил, т.е. равен элементарному приращению потенциальной энергии dE_k.       Правая часть уравнения (3.13) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем:                                                                                                   (3.14)       При переходе системы из состояния 1 в какое-либо состояние 2

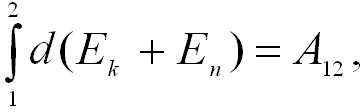т.е изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.14) следует, что

Откуда что и требовалось доказать.