46. Законы Бойля—Мариотта, Гей-Люссака и Шарля

М одель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давления» и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.

Рис. 2.1

Рассмотрим законы, описывающие поведение идеальных газов.

Закон Бойля—Мариотта*: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:

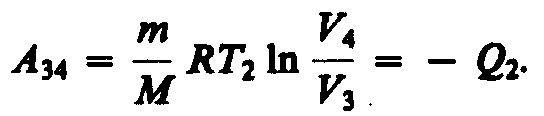
Хорошо известный закон Бойля-Мариотта был установлен английским физиком Бойлем в 1662 г. и независимо от него французским ученым Мариоттом в 1679 г.

Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная:

Процесс, происходящий при постоянной температуре, называется изотермическим. График этого процесса в координатах p – V представлен на рис. 2.1.

З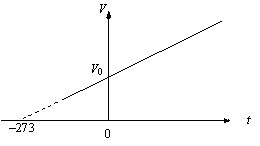 акон, связывающий объем газа V и его температуру t, измеренную в градусах Цельсия, был установлен французским ученым Гей-Люссаком в 1802 г.

Для данной массы m при постоянном давлении р объем газа линейно зависит от температуры:

г де V₀ – объем газа при нуле градусов Цельсия, α – коэффициент объемного расширения, t – температура по шкале Цельсия.

График этого процесса, называемого изобарическим, представлен на рис. 2.2. Коэффициент α для всех газов равен

Закон, связывающий давление газа р и его температуру t, установлен Шарлем.

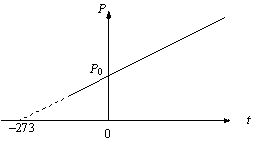Д ля данной массы m при постоянном объеме V давление газа линейно зависит от температуры:

,

где p₀ – давление газа при нуле градусов Цельсия, β – коэффициент объемного расширения, t – температура по шкале Цельсия.

График этого процесса, называемого изохорическим представлен на рис. 2.3. Коэффициент β длявсех газов равен

В координатах Р–V изобарический и изохорический процессы представлены на рис. 2.4.

Рис. 2.4

Опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. Однако когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов. Тем не менее, во многих случаях эти законы удобны для практического применения.

Если бы существовал газ, для которого не было бы отклонений от этих законов, то такой газ был бы идеальным газом.

47. Закон Авогадро, Закон Дальтона

Закон Авогадро*: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,4110^–3 м³/моль.

Согласно закону Авогадро различные газы, взятые в количестве 1 моль, имеют одинаковые объемы при одинаковых давлениях р и температурах t, так как число молекул в них одно и то же. При нормальных условиях, т. е. при температуре О °С и атмосферном давлении 101 325 Па, этот объем, как показывают измерения, равен  (3.8.1) Объем V_M0 называют молярным.

По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:

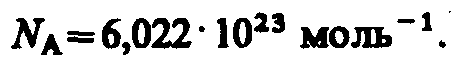
Закон Дальтона*: давление смеси идеальных газов равно сумме парциальных давлений p₁, p₂ ,..., р_n входящих в нее газов:

Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.

Английский химик Д. Дальтон установил, что для достаточно разреженных газов именно так и есть в действительности. Соотношение (3.8.2) называют законом Дальтона.

С точки зрения молекулярно-кинетической теории закон Дальтона выполняется потому, что взаимодействие между молекулами идеального газа пренебрежимо мало. Поэтому каждый газ оказывает на стенку сосуда такое давление, как если бы остальных газов не было.

 Моль любого газа при нормальных условиях занимает объем 22,4 л. Это значение объема установлено экспериментально. В смеси газов каждый из них оказывает давление на стенки сосуда независимо от присутствия других газов.