32. Кольца Ньютона и расчетная формула для радиусов темных колец Ньютона.

Классическим примером полос равной толщины являются кольца Ньютона. Они соблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластины и плоско-выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении- эллипсов. Найдем радиусы колец при нормальном падении света.

Т. к. , -для светлых, - для темных.

, чем больше m , тем теснее расположены кольца. Для светлых колец . Более точный результат, если брать разность двух колец .

33. Запишите формулу для числа зон Френеля при дифракции света на круглом отверстии или диске в случае сферического фронта волны. rm- радиуса зоны Френеля,

m – число зон,

34. Условия максимумов и минимумов интенсивности света при дифракции на од­ной щели. Приведите график зависимости интенсивности света от угла дифрак­ции при дифракции на одной щели. Френелевская дифракционная картина от щели представляет собой светлую или тёмную центральную полосу, по обе стороны которой распологаются симметричные относительно неё чередующиеся тёмные и светлые полосы. При большой ширине щели начало и конец результирующего вектора для точки Р лежат на внутренних витках спирали вблизи полюсов и . Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных узких светлых и тёмных полос. Как показывает формула ,расстояние минимумов от центра картины возрастает с уменьшением . Таким образом, с уменьшением ширины щели центральная светлая полоса расширяется, захватывая всё большую и большую область экрана.Если , то ,т.е. первый минимум соответствует углу ; следовательно, он сдвинут на бесконечно удалённый край экрана. Освещённость экрана падает от центра к краям постепенно, асимптотически приближаясь к нулю; ширина центральной световой полосы возрастает беспредельно.Таким образом, с уменьшением b освещённость стремится стать равномерной по всему экрану.(рис5)

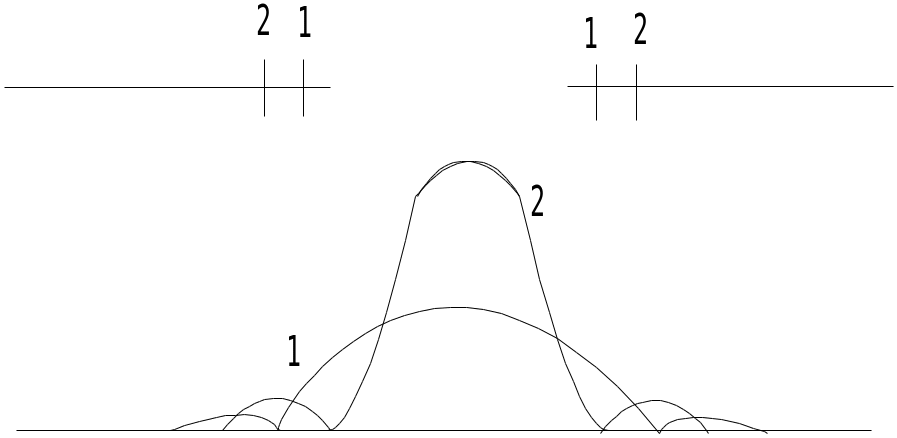
Наоборот, при увеличении ширины щели положение первых минимумов придвигается всё ближе и ближе к центру картины, так что центральный максимум становится всё резче и резче. При этом, относительная интенсивность максимума остаётся неизменной; абсолютная же величина его возрастает, ибо возрастает энергия, проходящая через уширенную щель.

35. Запишите условие главных максимумов интенсивности света при дифракции на дифракционной решетке (формулу дифракционной решетки). Приведите график зависимости интенсивности света от угла дифракции.

Т аким образом мы имеем максимум дифракции для направлений, удовлетворяющих условию:

d · sin φ = ±m · λ , где m - порядок спектра, φ - угол дифракции.

3 6. Условие максимумов интенсивности при дифракции рентгеновских лучей на пространственной решетке (формулу Вульфа-Брэгтов).. Вульф и Брэг наблюдали дифракцию на монокристале рентгеновских лучей. Согласно им, дифракция на монокристале рентгеновских лучей – есть результат их отражения от параллельных кристаллографических плоскостей, т.е. плоскостей, в кото-

рых находятся узлы кристаллической

решетки. AA’, BB’ – соседние парал-

лельные кристаллографические

плоскости. При этом отражение имеет

место при таких условиях падения

(при углах скольжения θ) при которых отраженные волны 1’ и 2’ являются когерентными и для них выполняются условия max интереренции. ∆=kλ, k=1,2,3… Все среды для рентгеновских лучей являются прозрачными и n=1. ∆=|ED|+|DF|=2dsinθ, 2dsinθ=+ - kλ – формула Вульфа-Брэга. Это соотношение лежит в основе метода рентгеновского спектра, испускаемого рентгеновской трубкой.