74)Эффект Комптона.

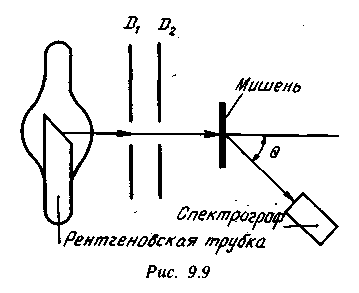
В 1923 г. американский физик А. Комптон (1892—1962) обнаружил, что при рассеянии монохроматических рентгеновских лучей «легкими» веще­ствами* наряду с исходной длиной волны Я в рассеянных лучах содержатся также лучи с большей длиной волны Я' (эффект Комптона). Схема опыта Комптона показана на рис. 9.9. Узкий пучок лучей, выделяемый диафрагмами di и D₂, падал на мишень из рассеивающего вещества. С помощью рентгеновского спектрографа измерялись длина волны λ' рассеянных под углом 0 лучей и их интенсивность. Было установлено, что разность Д λ = λ ' — Я не зависит ни от природы рассеивающего вещества, ни от длины Я падающих лучей, а зависит только от угла рассеяния б, образуемого/направлениями падающих и рассеянных лу­чей. Эта экспериментально найденная зависимость имеет следующий вид: — эффект Комптона,

λ_к—комптоновская длина волны.

Было также замечено, что интенсивность рассеянных лучей больше для веществ с малой атомной массой и мень­ше для веществ с большой атомной массой. Интенсивность рассеянного пучка растет с увеличением угла рассеяния Θ.

Обнаруженная на опыте независимость величины от рода вещества указывает на то, что рассеяние рентгеновских лучей происходит на внешних электронах атомов, которые слабо связаны с атомами рассеивающего вещества. Оцен­ки показывают, что энергия рентгеновских квантов значи­тельно больше энергии связи внешних электронов в ато­мах. Поэтому с достаточной степенью точности можно считать, что рассеяние рентгеновских квантов происходит на «свободных» электронах в отличие от фотонов, которые при фотоэффекте рассеиваются на «связанных» электро­нах (для фотона hv ~ A, A — работа выхода).

Для вывода формулы (9.31) предположим, что нале­тающий рентгеновский фотон упруго взаимодействует с покоящимся «свободным» электроном мишени (рис. 9.10, а). Поскольку энергия налетающего фотона сравнима с энергией покоя электрона hv~m₀c²), при использова­нии законов сохранения нужно энергию и импульс элек­трона определять по формулам релятивистской механики после

ввзаимодействия электрон начинает двигаться с некоторой скоростью (его называют электроном отдачи) под углом ф к направлению налетающего фотона (рис. 9.10, б), а рассеянный на угол 0 фотон будет иметь импульс РФ = М'.

В соответствии с законами сохранения импульса и энергии в системе фотон — электрон запишем систему двух уравнений (закон сохранения импульса графически иллюстрируется на рис. 9.10, в): — закон сохранения импульса;

(9.32) —закон сохранения энергии. Если из первого и второго уравнений системы выразить квадрат импульса электрона отдачи, то получатся следую­щие два уравнения:

Приравнивая эти выражения, получаем

Поскольку из формулы (9.35) после простых преобразований получим

Из сопоставления с зависимостью (9.31) получаем вы­ражение для комптоновской длины волны при рассеянии на электронах:

Из приведенных расчетов следует, что в эффекте Комптона отчетливо проявляются корпускулярные свойства света.