Обобщенный закон Гука

Обобщенный закон Гука для объемного напряженного состояния записывается (в главных напряжениях):

= ,

=

= .

Относительное изменение объема равно:

е = /Е.

Из этой формулы следует, что изменение объема не происходит (е = 0) в двух случаях:

если 1 - 2µ = 0, т.е. при µ = 0,5;

если .

При растяжении ; . Поэтому растяжение сопровождается увеличением объема е > 0.

При сжатии , получим е < 0. Следовательно, при сжатии стержня его объем уменьшается.

Чистый сдвиг ; . Таким образом имеем, что при чистом сдвиге объем тела не меняется.

Потенциальная энергия изменения формы

Потенциальная энергия упругой деформации может быть представлена как сумма энергий изменения формы и энергии изменения объема (рис. 2.3).

Рис. 2.3

Энергия изменения объема – это гидростатическая часть (всестороннее растяжение или сжатие) выделяемая из общего напряженного состояния. Величина напряжения р равна:

p = .

Тогда:

; ; .

Вторая часть напряженного состояния , которая не меняется от добавления всестороннего растяжения или сжатия и определяет энергию изменения формы.

Потенциальная энергия изменения формы, выраженная через главные напряжения , , определяется по формуле:

.

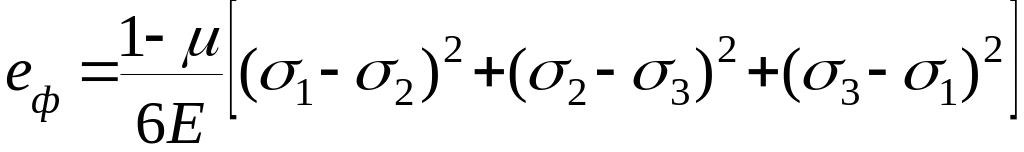Эквивалентное напряжение

Напряженное состояние в точке может быть задано главными напряжениями. В общем случае все они не равны нулю. Для расчета на прочность оно заменяется эквивалентным (равнопрочным, т.е. имеющим такой же запас прочности) одноосным растяжением, которое и рассчитывается на прочность (рис.2.4).

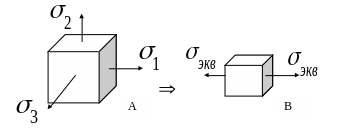
Состояние А равноопасно состоянию В

Рис. 2.4

Теории прочности

Переход от сложного напряженного состояния к эквивалент- ному осуществляется по теориям (гипотезам) прочности.

В сопротивлении материалов изучаются следующие теории прочности:

1) теория наибольших нормальных напряжений

= ; (2.4)

2) теория наибольших линейных деформаций

= - µ ( + ) ; (2.5)

3) теория наибольших касательных напряжений

= - ; (2.6)

4) теория удельной потенциальной энергии деформации изменения формы

= (1/ ) ; (2.7)

5) теория Мора

= - k , где k = 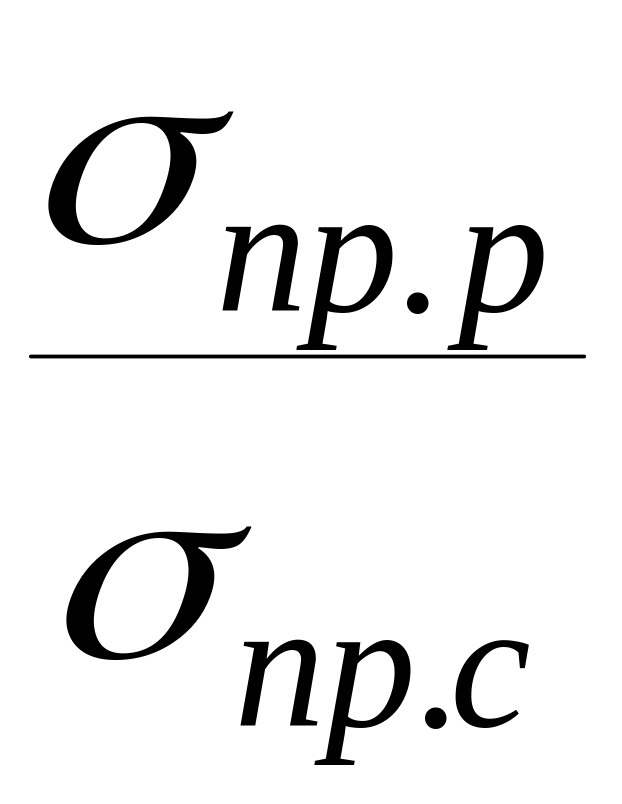. (2.8)

Здесь , предельные напряжения на растяжение и сжатие. В машиностроительных конструкциях часто встречаются детали, работающие на изгиб и кручение одновременно. В этом случае выделенный из детали элемент, находится под действием нормальных и касательных напряжений (рис. 2.5).

Рис. 2.5

При расчете пластичных материалов, одинаково сопротивля-ющихся растяжению и сжатию (обычные стали), в основном используют третью и четвертую теории прочности, а материалов с различными свойствами на растяжение и сжатие (закаленная сталь, чугун и др.) – теорию прочности Мора.

Для такого частного случая двухосного напряженного состояния, принимая в формуле (2.2) , , , получают расчетные формулы (2.6) –(2.8) в следующем виде:

Теория 3 = ; (2.9)

Теория 4 . = ; (2.10)

Теория 5 = 0.5 (1-k) + 0.5 (1+k) . (2.11)