37)Определение Производной

Производной ф-ции y=f(x) в тч. Х₀ наз. предел отношения приращения этой ф-ции к приращению аргумента , когда последнее стремится к нулю. если он сущ.

Формула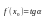 выражает геометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк.

Пусть f(x) определена на некотором промежутке (a, b). Тогда 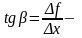тангенс угла наклона секущей МР к графику функ. , где  - угол наклона касательной к графику функ. f(x) в точке (x₀, f(x₀)). Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой:

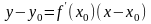
Уравнение нормали к кривой: .

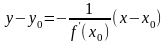экономический смысл производной. Пусть y(x) – ф-ция, характеризующая, напр., издержки производства, где x – колич. выпускаемой продукции. Тогда отношение 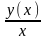описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af. Среднее приращение, средний прирост, средняя скорость изменения определяется отношением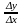 . Производная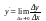 выражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.

_{38)Правила дифференцирования}: Обозначим f(x) = u, g(x) = v- функ., дифференцируемые в точке х.1.Производная сум.(разности) двух дифференц-ых ф-ций =сумме(разности) производных этих ф-ций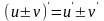 2.Производная произведения двух диффиренц-ых ф-ций = произведению первой ф-ции на производную второй + произведение второй ф-ции на производную первой: 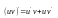3.Производная частного двух дифференц-ых ф-ций определ. формулой: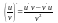 где

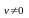
Производная сложной функции и обратной функций Производная сложной ф.: Есл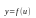и и -дифференцируемые ф. своих аргументов, то производная сложной ф. 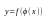сущ. и равна произведению производной этой ф-ции по промежуточному аргументу на производную промежуточного по независимой переменной, т.е. , .

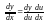Производная обратной ф.: Если y=f(x) и 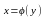- взимнообратые дифференцируемые ф-ции и 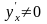,то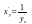 Действительно, т.к.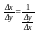 ,то

40 Дифференциал функции.

Пусть функция y = f(x) имеет конечную производную в точке х: 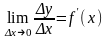, то

, где 0, при х0. f(x)x- линейная часть приращения и называется дифференциалом функции и обозначается dy df(x). dy = f(x)dx. Можно также записать:

Применение дифференциала к приближенным вычислениям.

Дифференциал функ. y = f(x) зависит от х и явл. главной частью приращения х.

Приращение ∆у функ. у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

∆у≈dy, ƒ(х+∆х) ≈ ƒ(х)+ƒ'(х) ∆х причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функ.

Дифференциал обычно находится значительно проще, чем приращение функ., поэтому формула широко применяется в вычислительной практике.