22. Многоцикловое нагружение. Основные понятия и определения.

Циклическое упругопластическое деформирование приводит к накоплению пластических деформаций, зависящих от числа циклов нагружения и амплитуды деформации в каждом цикле. Это накопление: может быть односторонним, монотонно нарастающим по мере увеличения циклов, или не приводящим к однонаправленному росту деформаций. Характер протекания пластических деформаций зависит от условий передачи нагрузки на деформируемый элемент, жесткости сопрягаемых деталей, а также от свойств материала. Накопление деформации при упругопластическом деформировании металлов с низкой частотой приводит к появлению повреждений (трещин) и, в конечном счете, к разрушению конструкций при многоцикловом (107—10е и более циклов) нагружении.

Многоцикловое усталостное разрушение происходит путем зарождения и развития усталостной трещины, когда макроскопическое пластическое деформирование и циклическая ползучесть практически отсутствуют. Однако в некоторых металлах при многоцикловом нагружении довольно интенсивно протекают процессы пластической деформации ( в общем случае неупругой деформации) в локальных объемах металла, что приводит к весьма значительным замкнутым петлям гистерезиса, площадь которых равна энергии, рассеянной в материале за цикл, а ширина - неупругой деформации за цикл. При малых неупругих деформациях практически отсутствует отличие в мягком и жестком режимах нагружения, при значительных неупругих деформациях их необходимо учитывать при оценке напряженно-деформированного состояния при наличии гоадиента напряжений и в других расчетах.

Сопротивление некоторого конструкционного материала многоцикловому усталостному разрушениюоценивают по кривой усталости, которая строится в координатах amax - N при данном коэффициенте асимметрии цикла R, иногда также в координатах а0 - N. Заштрихованы области 95% доверительной вероятности для средних значений долговечности.

2 3. Диаграмма предельных амплитуд. Факторы, влияющие на предел выносливости.

На величину предела выносливости образцов и деталей, изготовленных из одного и того же материала, кроме характеристик цикла нагружения влияет целый ряд различных факторов. Многочисленные эксперименты, проведенные с образцами различных форм и размеров, а также практика эксплуатации деталей машин показывают, что предел выносливости конкретной детали в значительной степени зависит от ее формы и размеров, от состояния поверхности и других обстоятельств.

Факторы:

• концентрация напряжений (K_σ);

• масштабный фактор, то есть влияние абсолютных размеров детали

• качество обработки поверхности (K_Fσ);

• эксплуатационные факторы (температ, коррозия, частота нагружения, радиационное облучение и т. д.);

• наличие поверхностного слоя, упрочненного различными технологически-

ми методами (K_V);

• анизотропия – неоднородность прочностных свойств материала.

σ_R – наибольшее (предельное) напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклов.

Обозначение предела выносливости для симметричного цикла – σ_–1, для от нулевого – σ₀.

Так как испытания нельзя проводить бесконечно большое время, то число циклов ограничивают некоторым пределом, который называют базовым числом циклов. В этом случае, если образец выдерживает базовое число циклов, то считается, что напряжение в нем не выше предела выносливости.

Д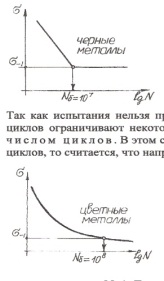 ля черных металлов базовое число циклов N_б=10⁷.

Кривые усталости для цветных металлов не имеют горизонтальных участков. Поэтому для них база испытаний увеличивается до N_б=10⁸ и устанавливается предел ограниченной выносливости (σ_–1N) для данной базы испытаний.

Предел выносливости при асимметричном цикле

И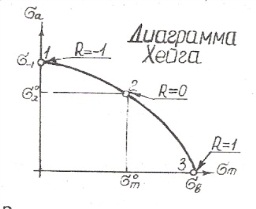 спытания при симметричном цикле (при R= -1) оказываются наиболее простыми с точки зрения их реализации. Однако в реальных конструкциях подавляющее число деталей работает при асимметричном нагружении. Поэтому, чтобы обеспечить корректность расчета, необходимы сведения о пределах выносливости для любой асимметрии цикла.

В расчетной практике обычно пользуются двумя типами диаграмм: диаграммой предельных напряжений и диаграммой предельных амплитуд.

Диаграмма предельных амплитуд [диаграмма Хейга

Д иаграмма предельных амплитуд строится в координатах: среднее напряжение цикла σ_m – амплитуда цикла σ_а. При этом для ее построения необходимо провести усталостные испытания так же, как минимум, для трех режимов: 1 – симметричный цикл нагружения (R= -1, σ_а=σ_--1, σ_m=0); 2 – отнулевой цикл (R=0, σ_a=σ_m=σ₀/2); 3 – статическое растяжение (R=1, σ_a=0, σ_m= σ_в). Соединяя экспериментальные точки (1, 2, 3) плавной кривой, получим график, характеризующий зависимость между значениями предельных амплитуд и значениями предельных средних напряжений в цикле.

Здесь также можем провести луч, характеризующий циклы с одинаковой асимметрией:

tgβ = σ_a /σ_m = (σ_max – σ_min)/(σ_max + σ_min) = (1 - R)/(1 + R)

Т огда, для определения предела выносливости при заданной асимметрии цикла R нужно по приведенной формуле вычислить величину угла β и провести луч под этим углом до пересечения с линией 1-2-3, ордината точки пересечения даст нам величину предельной амплитуды σ_a и значение предельного среднего напряжения σ_m в цикле. Предел выносливости σ_R найдем в виде

σ_R = σ_m + σ_a

25.Расчеты на выносливость при сложном нагружении (изгиб+кручение)

Совместные действия изгиба и кручения призматического стержня

Разлагаем все внешние силы на составляющие

P1x, P2x,..., Pnx и P1y, P2y,..., Pny.

который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору Мизг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру Мизг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость.

Р ис.2 Формирование результирующего изгибающего момента

Строим эпюру крутящего момента Мz.

Наибольшие напряжения изгиба возникают в точках k и k/, наиболее удаленных от нейтральной оси

где Wизг — момент сопротивления при изгибе.

В этих же точках имеют место и наибольшие касательные напряжения кручения

где Wр— момент сопротивления при кручении.

а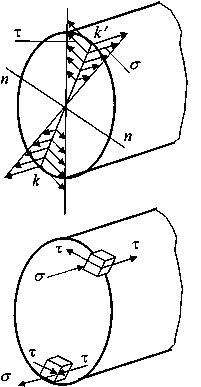 ) эпюры напряжений б) распределение напряжений

Если вал выполнен из пластичного материала, оценка его прочности должна быть произведена по одному из критериев текучести. Например, по критерию Треска—Сен-Венана имеем

Учитывая, что Wр=2 Wизг, для эквивалентных напряжений получаем

где —эквивалентный момент, с введением которого задача расчета вала на совместное действие изгиба и кручения, сводится к расчету на эквивалентный изгиб.

А налогично для Мэкв по.критерию Губера—Мизеса получаем

Т огда условие прочности для вала из пластичного материала будет иметь вид

Для стержня из хрупкого материала условие прочности следует записать в виде

где Мэкв должен быть записан применительно к одному из критериев хрупкого разрушения. Например, по критерию Мора

где .