14.Удельная потенциальная энергия деформации и ее составляющие

При простом растяжении (сжатии) потенциальная энергия

U= .

Удельная потенциальная энергия — количество потенциальной энергии, накапливаемое в единице объема: u = ; . В общем случае объемного напряженного состояния, когда действуют три главных напряжения:

или

Полная энергия деформации, накапливаемая в единице объема, может рассматриваться как состоящая из двух частей: 1) энергии u_o, накапливаемой за счет изменения объема (т.е. одинакового изменения всех размеров кубика без изменения кубической формы) и 2) энергии u_ф, связанной с изменением формы кубика (т.е. энергии, расходуемой на превращение кубика в параллелепипед). u = u_о + u_ф.

;

— тензор напряжений (матрица третьего порядка).

При переходе к главным напряжениям тензор напряжений получает вид:

При повороте системы координат коэффициенты тензора меняются, сам тензор остается постоянным.

Три инварианта напряженного состояния:

I₂= ;

I₃= ;

Аналогичные зависимости возникают при рассмотрении деформированного состояния в точке. Сопоставление зависимостей напряженного и деформированного плоского состояния (аналогия):

_ — относительная деформация, _ — угол сдвига.

Та же аналогия сохраняется и для объемного состояния. Поэтому имеем инварианты деформированного состояния:

J₁= _x + _y + _z;

J₂= _x_y +_y_z + _z_x — ²_xy — ²_yz — ²_zx;

— тензор деформаций.

_x, _y, _z, _xy, _yz, _zx — компоненты деформированного состояния.

Для осей, совпадающих с направлениями главных деформаций ₁, ₂, ₃, тензор деформаций принимает вид:

21.Понятие о контактных напряжениях.

К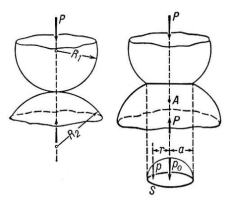 онтактные напряжения, напряжения, которые возникают при механических взаимодействии твёрдых деформируемых тел на площадках их соприкасания и вблизи этих площадок (например,при сжатии соприкасающихся тел).

p0 — максимальное напряжение в центре площадки контакта S; p — напряжение на расстоянии r от центра этой площадки; А — точка, в которой напряжение максимально.">

Распределение напряжений при сжатии сферических тел: Р — сжимающая сила; R1 и R2 — радиусы шаров; p0 — максимальное напряжение в центре площадки контакта S; p — напряжение на расстоянии r от центра этой площадки; А — точка, в которой напряжение максимально.

Контактные напряжения быстро убывают при достаточном удалении от места контакта (соприкасания тел). Распределение Контактные напряжения по площадке контакта и в её окрестности неравномерно и характеризуется большими градиентами, причём максимальные касательные напряжения tmax, которые в значительной мере предопределяют прочность сжимаемых тел (например, при сжатии шаров или пересекающихся цилиндров), имеют место на некоторой глубине (точка А) под площадкой контакта. Вблизи самой этой площадки напряжённое состояние близко к гидростатическому сжатию, при котором, как известно, касательные напряжения отсутствуют.

Проверка прочности при контактных напряжениях

Учитывая «мягкость» напряженного состояния в опасных точках (все три главных напряжения — сжимающие), проверку прочности при контактных напряжениях следует производить по третьей или четвертой теориям прочности:

Внося в эти формулы значения главных напряжений в опасной точке, выраженные через наибольшее напряжение в центре площадки контакта, условия прочности можно записать в следующем виде:

откуда

Здесь — допускаемое значение для наибольшего напряжения в месте контакта.

Значение коэффициента m зависит от отношений полуосей эллиптической площадки контакта и выбранной теории прочности.