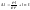- •2.Косой изгиб.
- •4.Статич-ки неопред-ые задачи при изгибе.Метод сил.
- •5.Внецентренное растяжение-сжатие.
- •8. Последовательность решения статически неопределимых задач.
- •6) Расчет плоских кривых брусьев (стержней)
- •9.Классификация напряженного состояния в точке тела.
- •10) Те́нзор напряже́ний,шаровой тензор,девиатор напряжений
- •13.Деформированное состояние в точке тела.
- •15.Расчеты на прочность при сложном напряженном состоянии.
- •19.Теория прочности Мора.
- •16.Теория наибольших нормальных напряжений.
- •17.Теория наибольших касательных напряжений
- •20)Концентрация напряжений. Влияние на прочность при статическом нагружении
- •18)Энергетическая теория прочности
- •14.Удельная потенциальная энергия деформации и ее составляющие
- •21.Понятие о контактных напряжениях.
- •22. Многоцикловое нагружение. Основные понятия и определения.
- •2 3. Диаграмма предельных амплитуд. Факторы, влияющие на предел выносливости.
- •7.Расчет статически определимых плоских и плоскопространственных стержневых систем
- •28)Внутренние силы, вызванные движением. Расчет поступательно движущихся систем.
- •29)Расчет вращающегося тонкостенного кольца.
- •30)Удар. Метод решения задач.
- •31)Приведенная масса.
- •32)Колебания упругих систем. Собственная частота колебаний.
- •34)Формула Ясинского-Тетмайера.
- •26 Расчет тонкостенных осесимметричных конструкций, нагруженных внутренним давлением
- •36)Механика хрупкого разрушения. Расчеты за пределами упругости.
- •27)Расчет трубы с толстыми стенками (задача Ляме)
- •24)Расчеты на выносливость при простых видах нагружения (растяжение, кручение, изгиб).
19.Теория прочности Мора.

O3F/O2 D=O1O3/O1O2 O3F=O2K-KF=R-Rp ,Rp=[σ]p/2, Rc=[σ]c/2, , R=(σ1 –σ2)/2
O2D=Rc-Rp , O3D=(σ1-σ2)/2-[σ]p/2=(σ1-σ2-[σ]p)/2

O2D=[σ]c/2-[σ]p/2=([σ]c-[σ]p)/2 O1O2=([σ]c+[σ]p)/2 O1O2= Rc+Rp
O1O3=O1O-OO3=Rp-(σ1+σ2)/2=[σ]p/2-(σ1-σ3)/2 O1O3=([σ]p-(σ1+σ3))/2
(σ1-σ3-[σ]p)/ ([σ]c-[σ]p)= (-(σ1+σ3)+[σ]p)/ ([σ]c+[σ]p)
σ1[σ]p+σ1[σ]c-σ3[σ]p-σ3[σ]c-[σ]p2-[σ]p[σ]c= [σ]p[σ]c -σ1[σ]c-σ3[σ]c-[σ]p2+σ1[σ]p+σ3[σ]p
2σ1[σ]c -2σ3[σ]p=2 [σ]p[σ]c/ [σ]c, σ1 -σ3[σ]p/[σ]c=[σ]р
σ1 -σ3[σ]p/[σ]c—σэ по5 теории σ1 -σ3[σ]p/[σ]c<=[σ]р σ1 -νσ3<=[σ]р-5теор.
![]()
ν=[σ]p/[σ]c
τ=σ1<=[σ] =>[τ]=[σ]--- из 1-ой теории τ-μ(ο-τ)<=[σ]
τ(1+μ)<=[σ], [τ]=[σ]/(1+μ)---из 2-ой теор
3-я: τ-(-τ)<=[σ], 2τ<=[σ] [-τ]=[σ]/2, 4-ая теор. прочности
![]()
1/21/2*((τ-ο)2+(ο+τ)2+4τ2)1/2=[σ], 1/21/2*(6τ2)1/2<=[σ],
τ*31/2 <=[σ], [τ]=[σ]/31/2, τ-ν(-τ)<=[σ]p, τ(1-ν)<=[σ]p, [τ]=[σ]p/(1+ ν)
σ=(μx- y)/Jx , τ=QSотс/ Jb
16.Теория наибольших нормальных напряжений.
В![]() общем случае опасное напряженное
состояние элемента конструкции зависит
от соотношения между тремя главными
напряжениями (1,2,3).
Т.е., строго говоря, для каждого соотношения
нужно экспериментально определять
величину предельного напряжения, что
нереально. Поэтому были приняты такие
методы расчета прочности, которые
позволяли бы оценить степень опасности
любого напряженного состояния по
напряжению растяжения – сжатия. Они
называются теориями прочности (теории
предельных напряженных состояний).
общем случае опасное напряженное
состояние элемента конструкции зависит
от соотношения между тремя главными
напряжениями (1,2,3).
Т.е., строго говоря, для каждого соотношения
нужно экспериментально определять
величину предельного напряжения, что
нереально. Поэтому были приняты такие
методы расчета прочности, которые
позволяли бы оценить степень опасности
любого напряженного состояния по
напряжению растяжения – сжатия. Они
называются теориями прочности (теории
предельных напряженных состояний).
1-ая теория прочности (теория наибольших нормальных напряжений): причиной наступления предельного напряженного состояния являются наибольшие нормальные напряжения. max= 1 []. Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.
![]() Теория
наибольших относительных удлинений
Теория
наибольших относительных удлинений
Рассм.
однородный стержень с одним концом,
жестко заделанным, и другим свободным,
к которому прилож. централ. продол. сила
Р
(рис. 2.2). До нагружения стержня его
длина равн. l после
нагружения она стала равной l + l
(рис. 2.2). Вел-ну l
называют абсолют. удлинением стержня.
Рис. 2.2 Если в нагружен. стержне
напряженное состояние является
однородным, т.е. все участки стержня
находятся в одинаковых условиях,
деформация
остается одной и той же по длине стержня
и равной
 (2.1)
Если же по длине стержня возник.
неоднород. напряжен. состоян., то для
определ. его абсолют. удлин. необход.
рассмотр. бесконечно малый элемент
длиной dz
(рис. 2.2). При растяж. он увеличит свою
длину на величину dz
и его деформация составит:
(2.1)
Если же по длине стержня возник.
неоднород. напряжен. состоян., то для
определ. его абсолют. удлин. необход.
рассмотр. бесконечно малый элемент
длиной dz
(рис. 2.2). При растяж. он увеличит свою
длину на величину dz
и его деформация составит:
 .(2.2)В
пределах малых деформаций при простом
растяжении или сжатии закон Гука
записывается в следующем виде: = E .
(2.3) Величина Е
представляет собой коэфф. пропорц.,
называем. модулем упруг. матер.-ла
первого рода. Из совместного рассмотрения
уравнений (2.2) и (2.3) получим:
.(2.2)В
пределах малых деформаций при простом
растяжении или сжатии закон Гука
записывается в следующем виде: = E .
(2.3) Величина Е
представляет собой коэфф. пропорц.,
называем. модулем упруг. матер.-ла
первого рода. Из совместного рассмотрения
уравнений (2.2) и (2.3) получим:
 откуда с учетом того, что
откуда с учетом того, что и
и
 ,окончательно
получим:
,окончательно
получим:
 (2.4)
(2.4)
Если
стержень изготовлен из однород.
изотропного материала с Е = const,
имеет постоянное поперечное сечение
F = const
и нагружен по концам силой Р,
то из (2.4) получим (2.5)При
решении многих практических задач
возникает необходимость, наряду с
удлинениями, обусловленными действием
механических нагрузок, учитывать
также удлинения, вызванные температурным
воздействием. В этом случае пользуются
принципом независимости действия
сил, и полные деформации рассматривают
как сумму силовой и температурной
деформаций:
(2.5)При
решении многих практических задач
возникает необходимость, наряду с
удлинениями, обусловленными действием
механических нагрузок, учитывать
также удлинения, вызванные температурным
воздействием. В этом случае пользуются
принципом независимости действия
сил, и полные деформации рассматривают
как сумму силовой и температурной
деформаций:
 (2.6)где
коэффициент
температурного расширения материала;
t перепад
температуры тела. Для однородного
стержня, нагруженного по концам
продольными силами Р
и равномерно нагретого по длине, получим:
(2.6)где
коэффициент
температурного расширения материала;
t перепад
температуры тела. Для однородного
стержня, нагруженного по концам
продольными силами Р
и равномерно нагретого по длине, получим: