10) Те́нзор напряже́ний,шаровой тензор,девиатор напряжений

Те́нзор напряже́ний — тензор второго ранга, состоящий из девяти величин, представляющих механические напряжения в произвольной точке нагруженного тела. Эти девять величин записываются в виде таблицы, в которой по главной диагонали стоят нормальные напряжения в трёх взаимно перпендикулярных осях, а в остальных позициях — касательные напряжения, действующие на трёх взаимно перпендикулярных плоскостях.

Рассмотрим напряженное состояние, при котором на трех взаимно перпендикулярных площадках действуют только три одинаковых главных напряжения

Т акое напряженное состояние описывается тензором который называется шаровым тензором напряжений.

При вычитании шарового тензора из тензора напряжений получается новый тензор, который называется девиатором напряжений:

Таким образом, тензор напряжений в любой точке тела может быть представлен в виде суммы шарового тензора и девиатора напряжений:

Шаровой тензор выделяет из напряженного состояния равномерное всестороннее растяжение (сжатие), при котором изменяется только объем данного элемента без изменения его формы. Девиатор напряжений характеризует состояние сдвига, при котором изменяется форма элемента без изменения его объема.

Первый инвариант шарового тензора напряжений S s совпадает с первым инвариантом тензора напряжений T s

Первый инвариант девиатора напряжений равен нулю. Действительно

.

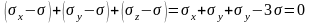Для определения второго инварианта, девиатора напряжений воспользуемся выражением для J 2 подставив в него вместо напряжений разности координатных и средних напряжений. После несложных преобразований получим или в главных напряжениях

Приведенные здесь зависимости понадобятся в дальнейшем, при формировании моделей упругости и пластичности.

11. Если по граням выделенного элементарного параллелепипеда действуют одни только нормальные напряжения, то они называются главными напряжениями, а площадки, на которых они действуют, называются главными площадками. Для определения главных напряжений предположим, что площадка abc является главной площадкой. Тогда на ней будут действовать только нормальные напряжения, то есть главные напряжения будут равны полным напряжениям p. В этом случае компоненты вектора полного напряжения p1, p2, p3 можно рассматривать как проекции главных напряжений на оси координат:

.

Подставив это условие в уравнение, получим

.

Эти уравнения можно рассматривать как систему линейных однородных уравнений относительно направляющих косинусов. В силу известного соотношения:

направляющие косинусы не могут одновременно иметь нулевые значения. В этом случае определитель, составленный из коэффициентов системы должен быть равен нулю:

Раскрыв определитель, получим характеристическое уравнение третьего порядка:

, где коэффициенты

называются инвариантами напряженного состояния в точке, так как они не изменяют своей величины при изменении направления исходной системы прямоугольных координат. Можно доказать существование трех действительных корней уравнения .На основании этого можно считать, что в каждой точке тела, независимо от его формы и размеров, места приложения, вида и характера нагрузок, существует не более трех взаимно ортогональных главных напряжения.

Для определения положения главных площадок необходимо знать направляющие косинусы нормали к этой площадке. Для их определения следует воспользоваться системой уравнений . Однако равенство нулю определителя этой системы указывает на то, что не все уравнения системы являются линейно независимыми; одно из них есть следствие двух других. Чтобы сделать систему определенной, надо добавить к ней равенство . После этого число независимых уравнений становится достаточным для однозначного определения направляющих косинусов.

12)Теория прочности Мора Получена на основе кругов напряжений Мора. . Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [_p] и сжатие [_с] не одинаковы (чугун).

Для пластичных материалов [_p]=[_с] теория Мора превращается в 3-ю теорию.

Круг Мора (круг напряжений). Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси  из центра С луч под углом 2 (>0, то против час.стр.), находим точку D,координаты которой: _,_. Можно графически решать как прямую, так и обратную задачи. Tg 2α=-2_y/(_-_y)

1)Выбир-ем прямоуг-ю систему коор-т ( ,) так чтобы ось была // большему из напряж-й

2)На оси х отложить _ , _у с учетом знаков

3)В концах этих отрезков восст-ть перпендикуляры _у , _ух

4)Соеденить эти перпендикуляры и на полученном отрезке – диаметре построить окружность

5)отрезки , отсекаемые на оси х будут численно равны искомым гл-ым напряжеиям