27)Расчет трубы с толстыми стенками (задача Ляме)

Примером осесимметричной задачи является задача Ламе о толстостенной круглой трубе, находящейся под действием внутреннего   и внешнего   равномерных давлений (рис. 4.11).

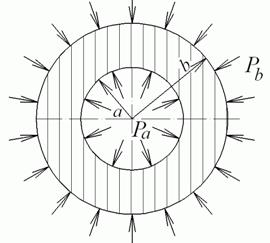
Рис. 4.11. Задача Ламе

Внутренний радиус трубы равен  , внешний —  .

Для решения воспользуемся формулами напряжений (4.35), полученными из общего решения осесимметричной задачи в перемещениях. Так как рассматриваемая задача относится к случаю плоской деформации, то указанные формулы должны включать упругие постоянные   и  . Согласно обозначениям (3.6), имеем

Для определения постоянных   и   имеем следующие условия на поверхности:

при  ;   

при  ;   

Подставляя их в формулы (а), получаем:

Решая совместно эти уравнения, находим:

После подстановки найденных постоянных в уравнения (а) напряжения:

(4.36)

Интересно отметить, что сумма нормальных напряжений   и   во всех точках трубы одинакова. Действительно, складывая почленно формулы (4.36), находим

.

(б)

В случае плоской деформации в поперечных сечениях трубы возникают также нормальные напряжения  . По аналогии с формулой (3.1),

Подставляя сюда сумму напряжений (б), получаем

.

Таким образом, осевые нормальные напряжения   постоянны по длине трубы. Исключение составляют сечения, находящиеся вблизи концов трубы, где, очевидно, труба не будет испытывать плоской деформации.

В частном случае, когда на трубу действует только внутреннее давление, т. е.  , формулы напряжений (4.36) принимают следующий вид:

(4.37)

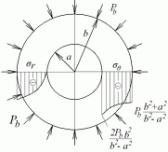
Эпюры этих напряжений изображены на рис. 4.12, а. Наибольшие сжимающие радиальные и растягивающие тангенциальные нормальные напряжения возникают в точках у внутренней поверхности трубы т. е. при  :

;

.

В точках у наружной поверхности трубы (при   )

а	б

Рис. 4.12. Эпюры при только внутреннем или только внешнем давлении

Рассмотрим трубу наружным радиусом, намного большим внутреннего. Из формул (4.37) после деления числителя и знаменателя на    получаем:

Переходя  к пределу при  , находим

(в)

Это значит, что все точки трубы испытывают одинаковые по значению радиальные и тангенциальные напряжения, отличающиеся лишь знаком. Следовательно, труба с бесконечно большим наружным радиусом находится в условиях чистого сдвига. В точках внутренней поверхности (при  )эти напряжения равны давлению  , а в точках, соответствующих  , они составляют  . Если в практических расчетах достаточна точность в 6%, то наружный радиус   можно считать бесконечно большим. В этом случае решение не связано с формой внешнего контура и формулы характеризуют распределение напряжений для трубы с любой формой внешнего контура при условии, что все его точки отстоят от центра отверстия на расстоянии, большем  ,

В другом частном случае, когда на трубу действует только наружное давление ( ), из формул (4.36) получаем

(4.38)

Эпюры этих напряжений изображены на рис. 4.12, б. В точках внутренней поверхности  при 

;

а в точках наружной  поверхности при 

;

.