31)Приведенная масса.

- m - работа сил тяжести

; ; ; ;

; ; ; - перемещение от действия силы тяжести. Нагрузка прикладывается не динамически, а статически.

; ;

Т.к. ищем наибольший прогиб – выбираем знак «+».

- коэффициент динамичности при ударе.

; ; ;

; ;

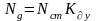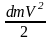- кинетическая энергия одной частицы.

; .

32)Колебания упругих систем. Собственная частота колебаний.

Теория колебаний представляет собой обширный раздел современной физики, охватывающий весьма широкий диапазон вопросов в области механики, электротехники, радиотехники, оптики и т.д. Особое значение имеет теория колебаний для прикладных задач, встречающихся в инженерной практике, в частности, в вопросах прочности машин и сооружений. Известны случаи, когда строительное сооружение, рассчитанное с большим запасом прочности на статическую нагрузку, разрушалось под действием сравнительно небольших периодически действующих сил. Во многих случаях жесткая и весьма прочная конструкций оказывается непригодной при наличии переменных сил, в то время как такая же более легкая, и на первый взгляд менее прочная, конструкция воспринимает эти усилия совершенно безболезненно. Поэтому вопросы колебаний и, вообще, поведения упругих систем под действием переменных нагрузок требуют от конструктора особого внимания.

При изучении колебаний упругие системы принято различать, прежде всего, по числу степеней свободы.

П од числом степеней свободы понимается число независимых координат, определяющих положение системы. Так, например, жесткая масса, связанная с пружиной (рис. 16.2), имеет одну степень свободы, поскольку ее положение определяется только одной координатой y. Это верно лишь в той мере, в какой имеется возможность пренебречь массой пружины по сравнению с массой колеблющегося груза. В противном случае, для того чтобы задать положение системы в любой момент времени, необходимо было бы ввести бесчисленное множество координат, определяющих положение всех точек упругой пружины, и система имела бы бесконечное число степеней свободы.

Для системы, изображенной на рис. 16.1, положение колеблющегося груза в плоскости чертежа определяется тремя независимыми координатами, например двумя координатами центра тяжести и углом поворота массы относительно центра тяжести. Следовательно, система имеет три степени свободы.

Любое реальное упругое тело имеет бесчисленное множество степеней свободы. Однако приближенно упругие тела можно рассматривать как предельный случай системы, состоящей из большого числа масс, соединенных между собой упругими связями.

Число степеней свободы определяется выбором расчетной схемы, то есть степенью приближения, с которой мы считаем необходимым или возможным исследовать реальный объект.

При исследовании упругих систем различают собственные и вынужденные колебания.

Под собственными колебаниями понимаются колебательные движения, которые совершает система, освобожденная от внешнего активного силового воздействия и предоставленная сама себе. Примером собственных колебаний являются, например, колебания ножек камертона. В этом случае движение происходит в результате начального импульса, сообщенного системе при ударе. Собственные колебания являются, как правило, затухающими.

Под вынужденными колебаниями понимается движение упругой системы, происходящее под действием изменяющихся внешних сил, называемых возмущающими. Примером вынужденных колебаний является движение, которое совершает упругое основание, если на нем установлен не полностью сбалансированный двигатель. В этом случае двигатель является источником энергии, периодически подаваемой в систему и расходуемой в процессе вынужденных колебаний на работу преодоления сил трения. Сила, действующая на упругое основание со стороны двигателя, является возмущающей силой.

Промежуток времени между двумя последующими максимальными отклонениями упругой системы от положения равновесия называется периодом колебаний и обозначается - T. Величина, ему обратная, называется частотой колебаний υ=1/T и представляет собой число колебаний в единицу времени. Частота измеряется в герцах (Гц) – числом колебаний в одну секунду. В технике вместо частоты υ используется в большинстве случаев круговая частота ω, представляющая собой число колебаний в 2π секунд, ω=2πυ=2π/T.

Амплитудой колебаний называется наибольшее смещение упругой системы от положения статического равновесия.

33). Термин устойчивость был введён в науку впервые Л.Эйлером. Приме-

нительно к упругим системам определение Эйлера можно сформулировать следующим образом: равновесие упругой системы при заданных внешних силах считается устойчивым в смысле Эйлера, если после статического

приложения и последующего снятия малой возмущающей силы система возвращается к своему исходному состоянию (рис. 9.3). В противном случае исходное состояние равновесия системы считается неустойчивым.

Другим, более общим, определением устойчивости состояния равнове-

сия является определение Лагранжа: исходное состояние равновесия упру-

гой системы устойчиво, если после отклонения её от этого состояния она, предоставленная самой себе, стремится вернуться к нему, совершая малые колебания, затухающие со временем при наличии сил внешнего и внутреннего сопротивления.

получаем формулу для критического значения силы (нагрузки бифуркации) Эйлера:

,где - приведённая длина Ясинского, 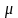- коэффициент приведения длины стержня к длине шарнирно опёртого по концам стержня.

Соответствующее критическое напряжение Эйлера:

где - гибкость стержня,

- радиус инерции площади поперечного сечения.