29)Расчет вращающегося тонкостенного кольца.
Рассмотрим случай вращения тонкостенного кольца (δ<<R) с постоянной угловой скоростью ω вокруг оси, перпендикулярной к плоскости кольца.
При вращении кольца каждый его элемент движется с центростремительным ускорением j=ω2R. Силы инерции направлены в сторону, противоположную ускорениям, и при постоянном сечении распределены равномерно вдоль кольца. Интенсивность сил инерции, т. е. сила инерции, приходящаяся на единицу длины кольца, q=Fρω2R. Здесь ρ - плотность материала, F - площадь сечения, а R - радиус средней линии кольца.
Кольцо теперь можно рассматривать как неподвижную плоскую раму, нагруженную равномерно распределенными радиальными силами интенсивностью q.
Рассекая кольцо любой диаметральной плоскостью на две части, приложим в сечениях осевые силы N и изгибающие моменты X1.
Рис. 14.5.
Проектируя все силы, действующие на полукольцо, на направление оси y, получаем
Отсюда
Подставляя в это выражение значение q, находим
Для определения неизвестного X1 составим каноническое уравнение
коэффициенты которого вычислим способом Мора.
Изгибающий момент в текущем сечении полукольца от силы N и распределенной нагрузки q (см. рис. 14.5, б)
а от единичной пары M1j=+1.
Следовательно, δ1P=0 и поэтому X1=0, т. е. изгибающие моменты во всех поперечных сечениях кольца равны нулю. Этот результат объясняется тем, что при вращении вокруг центра кольцо сохраняет свою форму и никаких изгибных деформаций не испытывает; увеличивается только его диаметр.
Таким образом, нормальные напряжения в поперечном сечении кольца
(14.2)
Например, в стальном кольце (ρ=7850 кг/м3) радиуса R=50 см при n=2500 об/мин растягивающее напряжение
Итак, напряжения во вращающемся кольце зависят только от окружной скорости v=ωR и плотности материала, но не зависят от площади его поперечного сечения. Поэтому увеличением размеров сечения нельзя уменьшить напряжения в тонкостенном вращающемся кольце.
Рассмотрим теперь случай равномерного вращения тонкостенного кольца вокруг его горизонтальной оси x.
Различные элементы кольца находятся на разных расстояниях от оси вращения, и поэтому силы инерции распределены неравномерно по длине кольца (рис. 14.6, a):
Максимальная интенсивность q=ρFω2R. Следовательно,
В сечениях вдоль вертикальной оси симметрии кольца будут действовать только изгибающие моменты X1, а перерезывающие силы Q и нормальные силы N равны нулю. В отсутствии нормальных сил N в этих сечениях легко убедиться, спроектировав все силы, действующие на левое или правое полукольцо, на горизонтальную ось симметрии.
Представим эквивалентную систему, как показано на рис. 14.6,б. Изгибающий момент в текущем сечении кольца от внешней нагрузки
а от единичной пары M1j+1.
Рис. 14.6. Рис. 14.7.
Составим каноническое уравнение
Коэффициенты δ1P и δ11 этого уравнения:
Следовательно,
Итак, изгибающий момент в текущем сечении рамы
Эпюра изгибающих моментов представлена на рис. 14.7. Опасными являются сечения A и B кольца, так как в этих сечениях кроме изгибающих моментов M=qR2/4 действуют наибольшие растягивающие нормальные силы
Максимальные напряжения в раме
где Wz - момент сопротивления изгибу, а F - площадь поперечного сечения кольца.
Расчет равномерно вращающегося прямого бруса.
Предположим, что прямой брус постоянного поперечного сечения с подвешенным грузом равномерно вращается вокруг оси, перпендикулярной плоскости чертежа (рис. 14.8). Определим напряжения в сечениях бруса.
Рис. 14.8.
При отсутствии вращения напряжения в поперечных сечениях бруса изменяются по линейному закону:
где ρ - плотность материала бруса; F - площадь поперечного сечения; G - вес груза.
Применяя принцип Даламбера, приложим к каждому элементу бруса силу инерции, равную массе этого элемента, умноженной на его центростремительное ускорение. Динамическая продольная сила будет равна:
После интегрирования динамически напряжения определяются по следующей формуле:
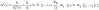
Напряжения изменяются по квадратичному закону и достигают максимума на оси вращения
Перемещение текущего сечения бруса
Полагая в этом выражении r=l, находим удлинение всего бруса, вызванное его вращением.
При отсутствии груза следует исключить в формулах величину G.
При вращении стержня относительно вертикальной оси (рис. 14.9) полученные выше формулы для динамических усилий, напряжений и перемещений нетрудно модифицировать. Так, например, динамические напряжения будут равны:
Рис. 14.9.
