28)Внутренние силы, вызванные движением. Расчет поступательно движущихся систем.

Для определения усилий, возникающих в движущемся теле или системе тел, наиболее удобно пользоваться принципом Даламбера. Применительно к рассматриваемым далее задачам этот принцип можно сформулировать следующим образом.

Если движущееся тело (систему тел) в какой-то момент времени представить себе находящимся в покое, но помимо сил, производящих движение, приложить к нему силы инерции, то в таком покоящемся теле будут существовать такие же внутренние усилия, напряжения и деформации, какие имеют место во время его движения.

Например, при вращении груза массой m, прикрепленного к проволоке длиной l, груз будет двигаться вокруг оси вращения с центростремительным ускорением j=v²/l=ω²l, вследствие чего в проволоке возникает растягивающее усилие. Сила инерции груза равна произведению массы груза на ускорение его движения и направлена в сторону, противоположную направлению ускорения :

,

где v - окружная скорость, ω=2πn/60 - угловая скорость движения груза, n - частота вращения груза (об/мин), l - радиус вращения (м), m - масса (кг).

Эта сила и вызывает равное ей усилие в проволоке. Сила натяжения проволоки - это вполне реальная сила, появляющаяся вследствие движения груза m с центростремительным ускорением j. Можно узнать, при какой частоте вращения проволока разорвется. Пусть масса груза m=0.1 кг, l=1 м, диаметр проволоки d=1 мм, а предел прочности материала проволоки σв=1500 МПа. Растягивающее напряжение в поперечном сечении проволоки

Проволока разорвется при σ=σв. Из этого условия находим предельную частоту вращения

Усилие, возникающее в проволоке в результате вращения груза, может быть определено на основании закона динамики неравномерно движущихся тел и без введения сил инерции. Действительно, центростремительное ускорение сообщается грузу проволокой. Следовательно, она действует на груз с центростремительной силой, равной произведению массы груза на его ускорение. Но по закону действия и противодействия такой же силой растягивается и сама проволока, поэтому усилие в ней

.

Таким образом, опираясь только на законы динамики, можно определить усилия, напряжения и деформации в любой неравномерно движущейся детали. Однако для практических целей удобнее пользоваться принципом Даламбера, так как он позволяет свести задачи динамики к задачам статики, методы решения которых подробно разработаны.

Расчет поступательно движущихся систем

Определим напряжения в канате грузоподъемного механизма, к которому подвешен груз массой m. При равномерном подъеме с постоянной скоростью ускорение движения груза равно нулю, поэтому напряжения в канате такие же, как и в том случае, когда груз висит на канате в состоянии покоя, т. е. σ=mg/G, где g - ускорение силы тяжести.

Во время разгона движение груза неравномерно, и в канате появляются дополнительные напряжения, для определения которых мысленно остановим груз и приложим к нему силу инерции. Эта сила направлена в сторону, противоположную движению груза и равна

где v - скорость подъема; w - ускорение.

Наибольшее усилие в канате соответствует моменту максимального ускорения груза во время разгона:

Следовательно, максимальное напряжение в канате при подъеме груза

больше напряжений при статическом приложении груза σ_cn=mg/F в k_д раз; коэффициент

называется динамическим коэффициентом.

Таким образом, для уменьшения растягивающего усилия в канате необходимо обеспечить плавное увеличение скорости подъема, так как при больших ускорениях напряжения в канате могут стать значительными. График изменения скорости в период разгона должен иметь вид: .

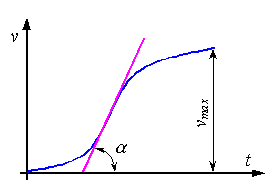Тангенс наибольшего угла α наклона касательной к этой кривой определяет максимальное ускорение движения груза во время подъема.

При опускании груза в начале движения величина w=dv/dt в выражении для kд будет иметь отрицательный знак. Следовательно, напряжения в канате в этом случае будут меньше напряжений от статического действия груза m.

Если канат длинный, то следует учесть массу самого каната и силы инерции его частиц. В этом случае опасным будет верхнее сечение каната, усилие в котором

где x - длина каната; ρ - плотность материала каната.

Рассмотрим горизонтальный брус, поднимаемый вверх силой S, приложенной посредине бруса (рис. 14.4,а).

Интенсивность полной погонной нагрузки, состоящей из собственного веса q бруса и инерционной нагрузки pi, определяется по формуле (рис. 14.4, б, в)

или

где G - вес бруса, w - ускорение бруса.

Сила S и нагрузка q_сумм вызывают изгиб бруса. Эпюры изгибающих моментов M и поперечных сил Q показаны на рис. 14.4, г, д.