3)поперечный изгиб балок

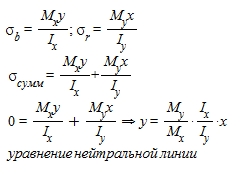
2.Косой изгиб.

Силовая пл-ть- пл-ть,проходящая ч\з продольную осьи одну из осей симметрии.

F_b =Fcosα F_г =Fsinα M_b =Mcosα M_г =Msinα

Напряжения в конструкции-сумма напряжений при изгибе в гориз. и вертик. пл-ти.

σ_y =M_x Y/J_x ; σ_x =M_y X/J_y ; σ=σ_x+σ_y = M_x Y/J_x + M_y X/J_y

σ=0-ур-ние нейтральной линии.

M_x Y/J_x + M_y X/J_y =0

Y=- -ур-ние нейтральной линии.

Положение нейтральной линии зависит от соотн. моментов инерции.Если Jx=Jy, то куда напр. наг-ка, туда направлено и перемещение. Косой изгиб-нагрузка действует под углом к главной оси.

4.Статич-ки неопред-ые задачи при изгибе.Метод сил.

С татически неопределимые системы – системы, силовые факторы в элементах которых не могут быть определены только из уравнений равновесия твердого тела. В таких системах число связей больше, чем необходимо для равновесия. Степень статической неопределимости: S = 3n – m, n – число замкнутых контуров в конструкции, m – число одиночных шарниров (шарнир, соединяющий два стержня, считается за один, соединяющий три стержня – за два и т.д.). Метод сил – в качестве неизвестных принимают силовые факторы. Суть этого метода заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и внутренних, а их действие заменяется соответ­ствующими силами и моментами. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной систе­мы.

К примеру рассмотрим дважды статически неопределимую систему. Заменим в основной системе действие отброшенных связей неизвестными усилиями X₁ и X₂ . Для их нахождения составляются канонические уравнения:

К оэффициенты находятся по формулам: , (i, j = 1,2). и

.

По закону парности коэффициентов

После решения канонических уравнений определяются величины неизве­стных усилий X₁ и X₂ .

5.Внецентренное растяжение-сжатие.

п о х-m, по y-n Под внецентренным растяжением-сжатием понимается такой вид нагружения, когда равнодействующая продольных сил смещена относительно оси бруса.

τ= ; M_x=Fm; M_y=Fn; σ=

Если сила приложена не к центру, то возникают моменты. Напряжение=сумме напряжений при изгибе и растяжении.

σ= ; ; i-радиус инерции.

Ядро сечения-геометр. место точек образ. фигуру, т.о. если сила нах-ся внутри этой фигуры, то напряжения по сечению имеют один и тот же знак.

Найдём ядро сечения на границе τ=0

σ_сж= ; σ_изг= ; W=πD³ /32

σ_min= -

Рассм. случай, когда сила F распол. на контуре.

σ=σ_сж σ_{изг ;} σ_сж= ; σ_изг= =

Напряж. изг. в раза больше напряж. сжатия За счёт изгиба могут возникнуть большие напряжения

8. Последовательность решения статически неопределимых задач.

Для раскрытия статической неопредели­мости наиболее широко применяются в инженерных расче­тах 2 метода: метод сил и метод перемеще­ний. В методе сил за основные неизвестные принимают обобщенные реактивные силы в отброшенных связях системы, а в методе перемещений в качестве неизвестных принимаются перемещения.

Метод сил:

1. Определяется степень статической неопределимости задачи путём подсчёта числа лишних связей.

2. Выбирается основная система, которая получается из заданной системы после удаления лишних связей. Удалённые связи заменяются лишними неизвестными усилиями.

3. Составляются уравнения перемещений, которые выражают условия совместимости перемещений основной системы с заданной статически неопределимой системой.

4. Решаются полученные ур-ния.

5. После определения лишних неизвестных находятся внутренние усилия в эл-тах статически неопределимой системы(изгибающие моменты, поперечные силы и т.д.)

Метод перемещений: Расчет кинематически неопределимых плоских рам методом перемещений производится в следующем порядке:

1. Рассчитывают общее количество неизвестных, 2. Принимают основную систему.

3. Составляют канонические уразнения.

4. Строят эпюры реактивных изгибающих моментов в стержнях принятой основной системы от единичных смещений по направлению неизвестных метода перемещений.

5. Строят эпюру изгибающих моментов в стержнях основной системы от всех внешних воздействий.

6. Вычисляют коэффициенты при неизвестных и свободные слагаемые канонических уравнений. 7. Выполняют проверку правильности расчета коэффициентов при неизвестных и свободных слагаемых канонических уравнений.

8. Решают систему линейных алгебраических уравнений и устанавливают истинные смещения узлов конструкции от заданных внешних воздействий.

9. Строят эпюру изгибающих моментов в заданной раме.

10. Выполняют проверку правильности построения эпюры изгибающих моментов способами: а) статическим; б) деформационным.