20) Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
Корреляционным
моментом
случайных величин X
и Y
называют математическое ожидание
произведения отклонений этих случайных
величин:
.
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей случайных величин X и Y.
Корреляционный момент служит для характеристики связи между случайными величинами X и Y.
Теорема. Корреляционный момент двух независимых случайных величин X и Y равен нулю.
Теорема. Абсолютная величина корреляционного момента двух случайных величин и не превосходит среднего геометрического их дисперсий:
Коэффициентом
корреляции
случайных величин X
и Y
называют отношение корреляционного
момента к произведению их средних
квадратических отклонений:
.
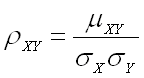Так
как размерность
равна произведению размерностей
случайных величин X,Y
и
, имеет размерность случайной величины
X,
, имеет размерность случайной величины
Y
, то
– безразмерная величина.
Теорема. Абсолютная величина коэффициента корреляции не превышает единицы:
.
21) Математическое ожидание и дисперсия функций случайных аргументов. Теоремы о числовых характеристиках функций случайных аргументов