15) Числовые характеристики статистического распределения

Генеральной средней xг называют среднее арифметическое значений

признака генеральной совокупности.

Выборочным средним xв называется среднее арифметическое всех значений

выборки:

x= x*p

Групповой средней называют среднее арифметическое значений признака,

принадлежащих группе.

Общей средней х называют среднее арифметическое значений признака,

принадлежащих всей совокупности.

Зная групповые средние и объемы групп, можно найти общую среднюю:

общая средняя равна средней арифметической групповых средних, взвешенной по

объемам групп.

Генеральной дисперсией Dг называют среднее арифметическое квадратов

отклонений значений признака генеральной совокупности от их среднего значения

x г .

Выборочной дисперсией Dв называется среднее арифметическое квадратов

отклонений значений выборки от выборочной средней xв

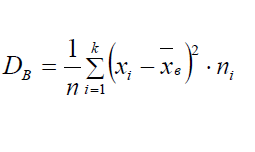
16)Выравнивание статистических рядов (метод моментов)

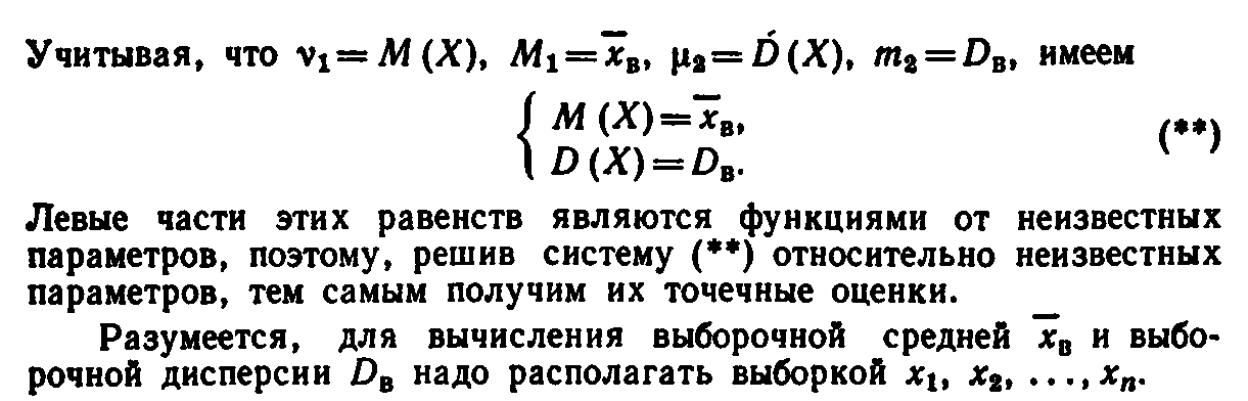
17) Критерии согласия

Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.

Обычно эмпирические и теоретические частоты различаются в силу того, что:

расхождение случайно и связано с ограниченным количеством наблюдений;

расхождение неслучайно и объясняется тем, что статистическая гипотеза о том, что генеральная совокупность распределена нормально — ошибочна.

Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду.

Эмпирические частоты получают в результате наблюдения. Теоретические частоты рассчитывают по формулам.

18) Понятие о системе случайных величин. Функция распределения и плотность распределения системы двух случайных величин

19)Законы распределения отдельных величин, входящих в систему. Условные законы распределения. Зависимые и независимые случайные величины

Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин входящих в систему.

Выразим теперь плотность распределения каждой из величин входящих в систему, через плотность распределения системы. Пользуясь формулой (8.3.5), выражающей функцию распределения через плотность распределения, напишем:

ткуда, дифференцируя по x , получим выражение для плотности распределения величины X:

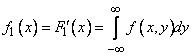
Аналогично

Таким образом, для того чтобы получить плотность распределения одной из величин, входящих в систему, нужно плотность распределения системы проинтегрировать в бесконечных пределах по аргументу, соответствующему другой случайной величине

Формулы (8.4.1), (8.4.2) и (8.4.3) дают возможность, зная закон распределения системы (заданный в виде функции распределения или плотности распределения), найти законы распределения отдельных величин, входящих в систему

Случайная величина Y называется независимой от случайной величины X, если закон распределения величины Y не зависит от того, какое значение приняла величина X.

Для непрерывных случайных величин условие независимости Y от X может быть записано в виде:

при любом y.

Напротив, в случае, если Y зависит от X , то