9) Моменты. Дисперсия. Среднее квадратическое отклонение

Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е.

σ(X) = .

Заметим, что размерность σ(х) совпадает с размерностью самой случайной величины Х, поэтому среднее квадратическое отклонение более удобно для характеристики рассеяния.

Обобщением основных числовых характеристик случайных величин является понятие моментов случайной величины.

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания

D(X) = M(X –М(Х))2.

Дисперсию случайной величины Х удобно вычислять по формуле:

а) для дискретной величины

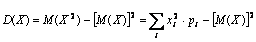
б) для непрерывной случайной величины

j(х)dx – [M(X)]^2

Дисперсия обладает следующими свойствами:

1. D(C) = 0, где С = const;

2. D(C×X) = C2∙D(X);

3. D(X±Y) = D(X) + D(Y), если X и Y независимые случайные величины.

10) Закон равномерной плотности. Закон Пуассона

Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:

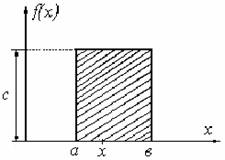
Говорят, что случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m , выражается формулой

где а – некоторая положительная величина, называемая параметром закона Пуассона.

вероятность возникновения случайного события n раз за время t.

11) Нормальный закон и его параметры. Моменты нормального распределения

Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

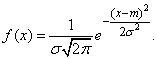
некоторые постоянные, называемые параметрами нормального распределения.

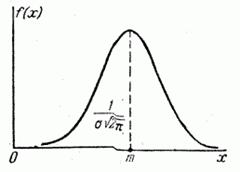
Выясним смысл параметров m и сигма нормального распределения. Непосредственно из формулы (6.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (x-m) на обратный выражение (6.1.1) не меняется. Если изменять центр рассеивания m, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.

Следовательно, параметр сигма в формуле (6.1.1) есть не что иное, как среднее квадратическое отклонение величины X

.

m-мат ожидание

Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что и , можно вычислить центральные моменты всех порядков. Так как , то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.

Для четных из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:

где под символом понимается произведение всех нечетных чисел от 1 до .