7) Функция распределения. Плотность распределения. Вероятность попадания случайной величины на заданный участок

Для непрерывной случайной величины невозможно составить закон распределения, поэтому для количественной характеристики удобно пользоваться не вероятностью отдельного события Х, а вероятностью события Х<x, где х – некоторая текущая переменная. Эти вероятности образуют некоторую функцию оси X.

F(x)=F(X<x)- интегральный закон распределения.

Плотность распределения - производная абсолютно непрерывной функции распределения.

Плотность распределения - производная абсолютно непрерывной функции распределения.

P(x<X<x+∆x)=F(x+∆x)-F(x)

P(α<x<β)=

F(x)=P(X<x)=P(-∞<X<x)

F(x)=

Основные свойства плотности распределения:

f(x)≥0

Д-во: Функция распределения – неубывающая функция, следовательно, ее производная – функция неотрицательная.

=1

Вероятность попадания случайной величины на заданный участок

При решении практических задач, связанных со случайными величинами, часто оказывается необходимым вычислять вероятность того, что случайная величина X примет значение, заключенное в некоторых пределах от α до β: α ≤ X < β.

Для определенности условимся левый конец α включать в участок (α, β), а правый нет: α ≤ Х < β.

Выразим вероятность этого события через функцию распределения величины Х. Для этого рассмотрим три события:

событие А, состоящее в том, что X < β;

событие В, состоящее в том, что X < α;

событие С, состоящее в том, что α ≤ Х < β.

Событие А по теореме сложения вероятностей равно А = В + С и его вероятность Р(А) = Р(В) + Р(С) или P(X < β) = P(X < α) + P (α ≤ Х < β). Но вероятность нахождения случайной величины левее некоторой текущей переменной есть ни что иное, как функция распределения:

F(β) = F(α) + P (α ≤ Х < β) откуда

P (α ≤ Х < β) = F(β) - F(α)

8) Числовые характеристики случайных величин. Характеристики положения (математическое ожидание, мода, медиана)

Числовые характеристики случайной величины – числа, суммарно описывающие случайную величину.

Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений:

. (2.4)

Для непрерывной случайной величины Х, имеющей заданную плотность распределения φ(x) математическим ожиданием называется следующий интеграл:

.

Отклонением называют разность между случ величиной и ее мат ожиданием.

Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис. 2.3), а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис. 2.4).

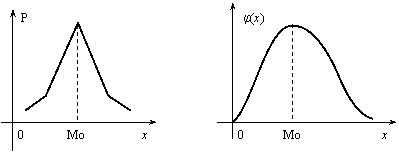
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.

Р(Х < Ме) = Р(X > Ме)