5)Частная и общая теоремы о повторении опытов
Вероятность
одного сложного события, состоящего в
том, что в n
испытаниях событие A
наступит ровно k
раз и не наступит n-k
раз, по теореме умножения вероятностей
независимых событий равна
.Таких
сложных событий может быть столько,
сколько можно составить сочетаний из
n
элементов по k
элементов, т.е.
.
Т.к. эти сложные события несовместны,
то по теореме сложения вероятностей
несовместных событий искомая вероятность
равно сумме вероятностей всех возможных
сложных событий. Поскольку вероятности
всех этих сложных событий одинаковы,
то искомая вероятность равна вероятности
одного сложного события, умноженной на
их число:
.
Эта формула называется формулой Бернулли.
Если
производятся n
независимых опытов в различных условиях,
причем вероятность появления события
А в i-м
опыте равна
то вероятность Р
того, что событие А в n
опытах появится m
раз, равна коэффициенту при Z
в
разложении по степеням Z
производящей функции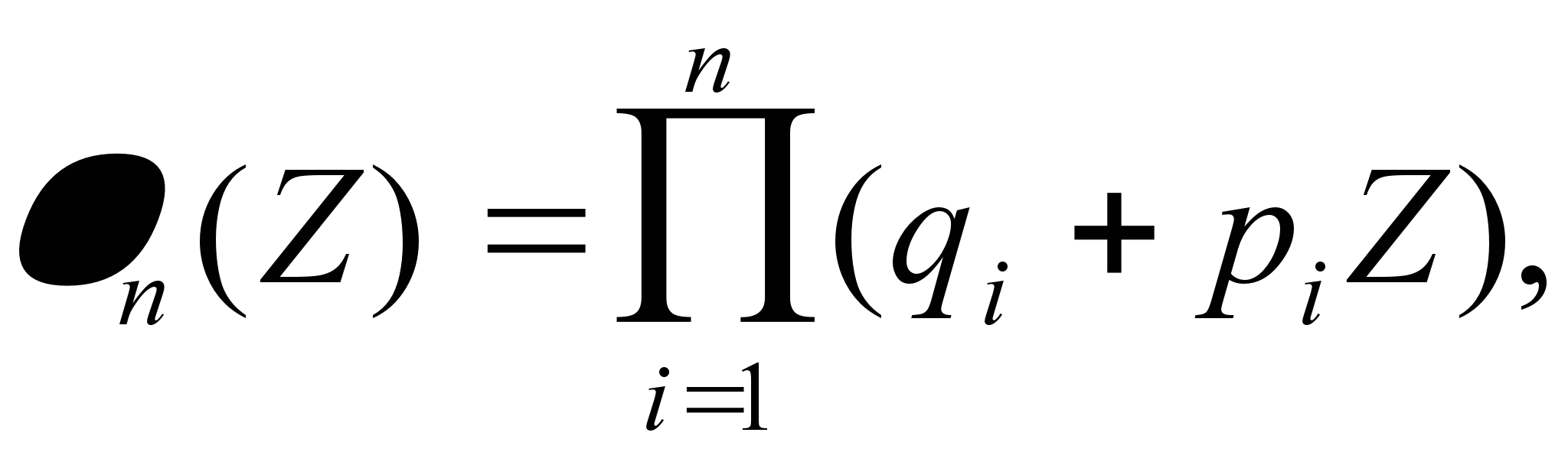
6) Случайные величины и их законы распределения. Ряд распределения. Многоугольник распределения
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее какое именно.
Случайные величины бывают двух типов:
• непрерывные;
• прерывные (дискретные).
Условимся в дальнейшем случайные величины обозначать большими буквами, а их возможные значения – соответствующими малыми буквами.
Пример:
Х- число попаданий при трех выстрелах:
х1 = 0;
х2 = 1;
х3 = 2;
х4 = 3.
Рассмотрим прерывную случайную величину Х с возможными значениями x1, x2, …, xn. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью
Х= х1;
Х= х2;
Х= х3;
Х= х4.
Обозначим вероятности этих событий P(X=x1) = p1; P(X=x2) = p2; P(X=xn)=pn.
∑Pm,n = 1, так как несовместные события образуют полную группу. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если будет задано это распределение, т.е. в точности указано, какой вероятностью обладает каждое из событий. Этим устанавливается так называемый закон распределения случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.Закон распределения прерывной случайной величины Х может быть задан в следующих формах:
• табличной;
• аналитической;
• графической.
Простейшей формой задания закона распределения прерывной случайной величины Х является таблица.
xi x1 x2 … xn
pi p1 p2 … pn
Такую таблицу называют рядом распределения случайной величины Х.
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению.
Для непрерывной случайной величины такой характеристики построить нельзя!!!
Для непрерывной случайной величины удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где х – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х и есть некоторая функция от х.
Эта функция называется функцией распределения случайной величины Х и обозначается F(х):
F(x) = P(X< x)
Функцию распределения F(x) называют также интегральной функцией распределения или интегральным законом распределения.
Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.
Сформулируем некоторые общие свойства функции распределения:
1.F(x) – неубывающая функция своего аргумента т.е. при x2 > x1 F(x2) > F(x1);
2. F(–∞) = 0;
3. F(+∞) = 1.