БИЛЕТ 1

1 .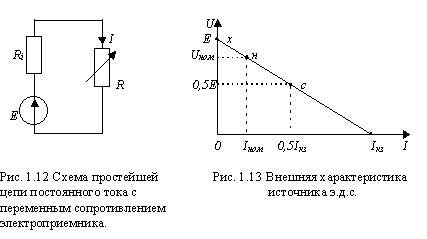

Билет 2

1. ур-е внешн хар-ки источника

Если (-) как генератор, (+) – аккумулятор

Обобщенный з-н Ома

если I и U совпадают то (+)

если I и E совпадают то (+)

2. Схема типа «звезда-звезда» без нулевого провода.

с помощью метода двух узлов.

.

Токи в ветвях определяются с помощью законов Ома:

;

;

.

Е сли нагрузка равномерная, то есть , то: , тогда: , , .

Рассмотрим схему типа «звезда-звезда» с нулевым проводом.

Токи 3х контурах: ; ; . Ток, через нулевой провод по первому закону Кирхгофа: . В случае равномерной (симметричной) нагрузки, при которой выполняется условие , нулевой ток равен нулю.

. В этом случае токи, текущие через линейный провода: , , .

Билет 3

1. Потенциальная диаграмма – график распределения потенциала вдоль участка цепи или замкнутого контура. По оси абсцисс откладывают величины сопротивлений, суммируя их. По оси ординат откладывают потенциалы точек цепи. Потенциал какой-нибудь одной точки можно принять за ноль и относительно него определять потенциалы других точек цепи.

2. Трёхфазная цепь – совокупность трёхфазной системы ЭДС, трёхфазной нагрузки и соединительных проводов.

Трёхфазного источника в цепях обозначается следующим образом:

Существует пять простейших способов соединения трёхфазного генератора с трёхфазной нагрузкой:

1. «Звезда-звезда» с нулевым проводом.

2. «Звезда-звезда» без нулевого провода.

3. «Звезда-треугольник»

4. «Треугольник-треугольник».

5. «Треугольник-звезда»

Нулевой провод – провод, соединяющий нулевые точки генератора и нагрузки.

Линейные провода – провода, соединяющие точки , и генератора и нагрузки.

Линейные токи – токи, текущие через линейные провода.

Линейные напряжения – напряжения между линейными проводами.

Фаза генератора – каждая и трёх обмоток генератора.

Фаза нагрузки – каждая из трёх нагрузок.

Фазовые токи – токи, протекающие через фазы генератора и нагрузки.

Фазовые напряжения – напряжения на фазах генератора и нагрузки.

Рассмотрим соединение типа «звезда-треугольник».

Т ок по следующей формуле: .

Аналогично можно найти токи, и .

Линейные токи: ; ; .

.

, , . Так как нагрузка равномерная: .

При равномерной нагрузке ;

;

.

Если нагрузка равномерная, то линейное напряжение равно фазовому ( ), а линейный ток больше в раз фазового ( ).

Билет 4

1. Метод свёртывания пассивных элементов

U=U₁+U₂+U₃, I общий.

R_ЭКВ=R₁+R₂+R₃

P_ЭКВ=I²/R_ЭКВ

R_ЭКВ=R₁R₂/R₁+R₂; 1/R_ЭКВ=1/R₁+1/R₂+…

G=1/R_ЭКВ - проводимость

P_ИС=UI

P_ПР=I₁²R₁+I₂²R₂, P=U²g₁+U²g₂

1. С помощью законов Кирхгофа

1й закон Кирхгофа: сумма токов в узле = 0.

2й закон Кирхгофа: алгебраическая сумма падений напряжений на резистивных элементах, составляющих замкнутый контур, равна алгебраической сумме ЭДС источников ЭДС этого контура.

UI=EI-I²R₀ – уравнение баланса мощностей,

UI-мощность приёмника

EI-мощность источника

I²R₀-потери внутри источника

2. Метод контурных токов

Алгоритм:

1. разбиваем схему на соприкасающиеся контуры, задаёмся направлением контурных токов

2. составляем уравнения для каждого из контуров: определяем контурные токи, а по ним – действительные токи ветвей.

3. метод двух узлов

напряжение между двумя узлами определяют по формуле: . ЭДС источников и токи источников тока, направленные к точке 1 войдут в эту формулу с положительным знаком, а ЭДС источников и токи источников тока, направленные к точке 2 войдут в эту формулу с отрицательным знаком.

Определяем токи в ветвях по закону Ома:

;

4. Преобразование пассивных элементов треугольника в эквивалентную звезду и наоборот

В узлах 1, 2, 3 и схема типа «звезда» и схема типа «треугольник» соединяются с остальной частью цепи. Часто есть необходимость преобразовать схему типа «звезда» в схему типа «треугольник» или наоборот схему типа «треугольник» в схему типа «звезда». Если преобразование выполнить так, что при одинаковых значениях потенциалов узлов, подтекающие к ним токи одинаковы, то на внешней цепи эта замена не отразится.

Переход от схемы типа «Звезда» к схеме типа «Треугольник» осуществляется по следующим формулам: ; ; . ;

2.