25 Основные элементы круговой кривой. Расчет
На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.
На железнодорожных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами СТН Ц-01-95.
Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами (рис. 83).
Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; середина круговой кривой СКК; конец круговой кривой ККК.
Основными элементами кривой являются:
1. Угол поворота трассы У.
2. Радиус закругления R.
Во время изысканий угол У вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НКК, О (рис. 83).
3. Тангенс кривой (касательная) Т – расстояние по прямой от вершины угла до начала или конца кривой.
4. Длина кривой К от начала кривой до её конца.
5. Биссектриса кривой Б – отрезок от вершины угла до середины кривой.
6. Домер Д – разность между длиной двух тангенсов и кривой.
Д = 2Т - К .
Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы для разбивки кривых.
Вычислить пикетажные значения главных точек кривой – значит узнать на каких пикетах и плюсовых точках они находятся.
Сначала определяют пикетаж вершины угла поворота ВУ, а затем находят пикетажное значение начала, конца и середины кривой
.
26 Детальная разбивка круговых кривых способом прямоугольных координат
По трем главным точкам точно построить кривую на местности невозможно, поэтому при строительстве трассы её обозначают рядом дополнительных точек. Данные работы называются детальной разбивкой кривой.
Расстояние между соседними точками на кривой К при детальной разбивке зависит от её радиуса R и характера сооружения, однако чем меньше R кривой, тем меньше значение К. при R > 500 м разбивку производят через промежутки k = 20 м, при 500 > R > 100 м k = 10 м, при R < 100 м k = 5 м.
Из всех существующих способов детальной разбивки, различающихся между собой по виду измерений и условиям использования, рассмотрим два способа.
Способ прямоугольных координат от тангенсов.
Пусть М – начало кривой радиуса R (рис.85). Примем тангенс МА за ось абсцисс, а радиус МО за ось ординат. Положение точки N, кривой в принятой системе координат определяется абсциссой X1 и ординатой Y1.
Если условимся производить разбивку через промежутки с длиной дуги k, то получим:
.
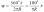Тогда для точек 2, 3 и т.д. координаты вычисляют, подставляя в вышеприведенные формулы углы 2j, 3j и т.д.
По указанным формулам составлены таблицы, из которых по аргументам R и k можно выбрать значение Х и У.
В виду того, что значения k и Х близки между собой, в таблицах часто вместо графы Х дают значения (k – Х), называемые «кривая без абсциссы». Разбивку кривой производят с двух сторон – от начала и конца к середине кривой. По тангенсам отмеряют значение k и от полученной точки в обратном направлении откладывают значение (k – Х). Из данной точки восстанавливают перпендикуляр и откладывают на нём ординату Y.
Достоинство способа прямоугольных координат состоит в том, что каждая точка кривой выносится независимо от других с примерно одинаковой точностью.
Детальную разбивку кривой способом прямоугольных координат удобно проводить в открытой и непересеченной местности.