2. Выбор типов шкал
Обосновать выбор типов шкал для каждого из случаев, определенных вариантом (таблица 2).
Таблица 6 – Номера объектов измерения
-
Вар.
Номера из табл. 3
10
1,12,28,37
Таблица 7 – Объекты измерения
№ |
Объекты |
1 |
Гербы |
12 |
Прибыль |
28 |
Деньги |
37 |
Районы Уфы |
Рассмотрим объекты измерения согласно варианту (табл. 2 и 3).
Герб – шкала наименования, поскольку идут только перечисления видов гербов, и не указываются какие-либо их характеристики, по которым возможно какое-либо сравнение гербов.
Прибыль–шкала отношений, поскольку используются числа, характеризующие отношение между интервалами. Нет отрицательных значений, а нулевое есть.
Деньги – шкала отношений, поскольку используются числа, характеризующие отношение между интервалами. Нет отрицательных значений, а нулевое есть.
Районы Уфы– шкала наименований, поскольку у каждого района свое уникальное имя и можно выполнять только одну операцию, выполняется только аксиома тождественности.
Примеры на каждый тип шкал:
Шкала наименований – название цветов;
Шкала порядка – загрязненность одежды;
Шкала интервалов – координатная прямая;
Шкала отношений – сопротивление резистора.
Вывод: В процессе выполнения данной работы были изучены различные типы шкал, а также методы правильного выбора и определения необходимого типа шкалы для разных случаев измерений.
3. Определение порядка проведения работ
Методом логического ранжирования обосновать порядок проведения работ.
Причинно-следственные связи между работами представлены в виде графа (см. варианты из таблицы 4). Каждой работе соответствует определенная длительность (таблица 5). Результатом выполнения работ является работа 0.
Выбранный порядок проведения работ должен быть оптимален в смысле минимальности затрат времени.
Таблица 4 – Дуги графа
Вариант |
Дуги графа |
|||||||||||||||||
9 |
Исх. |
1 |
2 |
2 |
3 |
4 |
5 |
5 |
6 |
7 |
7 |
8 |
8 |
8 |
9 |
10 |
10 |
11 |
|
Вх. |
0 |
0 |
3 |
1 |
2 |
3 |
4 |
1 |
6 |
9 |
7 |
10 |
5 |
6 |
9 |
11 |
5 |
Таблица 5 – Длительность работ
Вариант |
Работы |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
9 |
0,2 |
0,8 |
0,3 |
0,4 |
0,8 |
0,5 |
1 |
0,9 |
1 |
1 |
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
По исходным данным (табл. 4 и 5) строится граф.
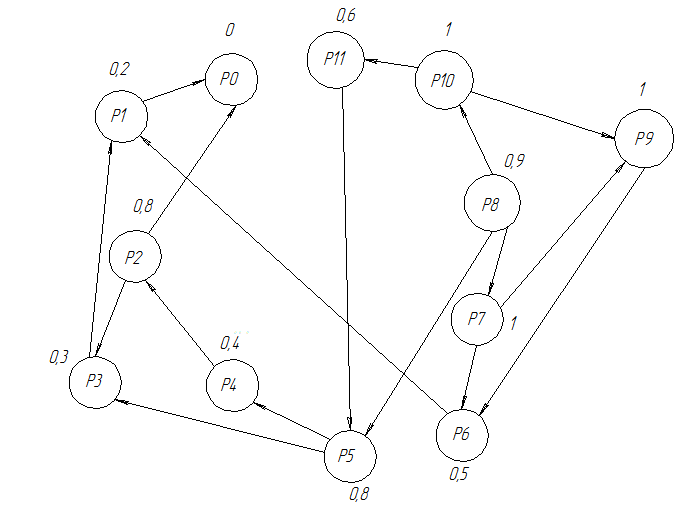
Рисунок 6 (К порядку проведения работ)
Для принятия решений используется 2 метода:
1 метод: определение важности или веса каждой из работ. Для принятия решения нужно выработать критерий, по которому будет производиться оптимизация. В качестве критерия возьмем вес работы. Чем больше вес, тем раньше работу нужно выполнить. Для решения данной заданной задачи составляем матрицу весов.
Таблица 10 – матрица весов
|
Р0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
Р8 |
Р9 |
Р10 |
Р11 |
∑ |
Р0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
Р1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
Р2 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
4 |
Р3 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
3 |
Р4 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
5 |
Р5 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
6 |
Р6 |
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
3 |
Р7 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
|
|
5 |
Р8 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
Р9 |
1 |
1 |
|
|
|
|
1 |
|
|
1 |
|
|
4 |
Р10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
10 |
Р11 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
1 |
7 |
2 метод: Определение времени, которое должно пройти от начала или завершения работы до завершения цикла всей работы. Для этого в матрицу весов вместо единиц записываются длительность работ, стоящих в заголовках столбцов.
Таблица 11
|
Р0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
Р8 |
Р9 |
Р10 |
Р11 |
∑ |
Р0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
Р1 |
0 |
0,2 |
|
|
|
|
|
|
|
|
|
|
0,2 |
Р2 |
0 |
0,2 |
0,8 |
0,3 |
|
|
|
|
|
|
|
|
1,3 |
Р3 |
0 |
0,1 |
|
0,3 |
|
|
|
|
|
|
|
|
0,4 |
Р4 |
0 |
0,2 |
0,8 |
0,3 |
0,4 |
|
|
|
|
|
|
|
1,7 |
Р5 |
0 |
0,2 |
0,8 |
0,3 |
0,4 |
0,8 |
|
|
|
|
|
|
2,5 |
Р6 |
0 |
0,2 |
|
|
|
|
0,5 |
|
|
|
|
|
0,7 |
Р7 |
0 |
0,2 |
|
|
|
|
0,5 |
1 |
|
1 |
|
|
2,7 |
Р8 |
0 |
0,2 |
0,8 |
0,3 |
0,4 |
0,8 |
0,5 |
1 |
0,9 |
1 |
1 |
0,6 |
7,5 |
Р9 |
0 |
0,2 |
|
|
|
|
0,5 |
|
|
1 |
|
|
1,7 |
Р10 |
0 |
0,2 |
0,8 |
0,3 |
0,4 |
0,8 |
0,5 |
|
|
1 |
1 |
0,6 |
5,6 |
Р11 |
0 |
0,2 |
0,8 |
0,3 |
0,4 |
0,8 |
|
|
|
|
|
0,6 |
3,1 |
Вывод: с помощью этого метода мы можем добиться упорядочивания этапов выполнения некоторых работ.