8.1 Определение реакций.

Составляются уравнения равновесия и определяются реакции Y_В и R_A:

0; M + Y_B*L – q*L*1.5L = 0

Y_B = (1.5q*L² – M)/L = (1.5*40*1 – 15)/1 = 45 кН;

0; M + R_A*L – q*L*0.5L = 0

R_A = (0.5q*L² – M)/L = (0.5*40*1 – 15)/1 = 5 кН;

0 Y_B – R_A – q*L = 45 – 5 – 40 = 0

Положительные значения реакций свидетельствуют о том, что первоначальное направление реакций выбрано верно.

7.2 Построение эпюр поперечных сил q и изгибающих моментов м.

Балка разбивается на черыти силовых участка. Составляются уравнения поперечных сил и изгибающих моментов на каждом участке:

1 – й участок.

Q₁ = q*z₁, 0 < z₁ < 1м

Q₁(0) = 0; Q₁(1) = q = 40 кН.

M₁ = – q*z₁* z₁/2, 0 < z₁ < 1м

M₁(0) = 0; M₁(1) = – 20 кНм.

2 – й участок.

Q₂ = q*L – Y_B = 40 – 45 = – 5 кН.

M₂ = – q*L* (L/2 + z₂) +Y_B* z₂, 0 < z₂ < 1м

M₂(0) = – 20кНм; M₂(1) = – 15 кНм.

3 – й участок.

Q₃ = 0.

M₃ = – M = – 15 кНм.

4 – й участок.

Q₄ = 0.

M₄ = 0.

По полученным значениям строятся эпюры Q и М.

8.3 Определение размеров поперечного сечения балки.

Из эпюры М определяется максимальное значение изгибающего момента. Рассчитывается требуемый момент сопротивления сечения из условия прочности по нормальным напряжениям [1, стр. 53]:

, (8.1)

где – момент сопротивления сечения [см³]; – максимальное значение изгибающего момента по модулю [кНм]; – допустимое нормальное напряжение [МПа].

= 0.25 *10^-3 м = 250 см³.

Определяются размеры сечений разной формы:

– определяются размеры сечения прямоугольной формы b,h для заданного соотношения h = 2b:

, [1, стр. 54] (8.2)

где – момент сопротивления сечения [см³]; h – высота прямоугольника [см]; b – ширина прямоугольника [см].

; b = = 7.21 см; h = 2*7.21 = 14.42 см;

– диаметр d круглого сечения:

, [1, стр. 54] (8.3)

где – момент сопротивления сечения [см³]; d – диаметр круглого сечения [см].

d = = 13.66 см;

– номер швеллера для сечения, состоящего из четырех швеллеров:

= 4*W_X, [1, стр. 54] (8.4)

где – момент сопротивления сечения [см³]; W_X – момент сопротивления сечения [см³].

W_X = /4 = 250/4 = 62.5 см³.

По таблице сортамента выбирается наиболее подходящий швеллер

№ 36:

= 4* , [1, стр. 54] (8.5)

где – момент сопротивления сечения [см³]; – момент сопротивления сечения по таблице сортамента [см³].

= 4*61.7 = 246.8 см³.

Поскольку момент сопротивления сечения несколько меньше требуемого, то необходимо определить перегрузку по напряжениям:

σ = M_max/ , [1, стр. 54] (8.6)

где σ – нормальное напряжение [МПа]; M_max – максимальный крутящий момент [кНм]; – момент сопротивления сечения [см³].

σ = 40*10³/246.8*10^-6 = 162 МПа;

Δσ = *100, [1, стр. 54] (8.7)

где Δσ – перегрузка по напряжениям [%]; – нормальное напряжение сечения; – допустимое напряжение.

Δσ = *100 = 1.3 %.

Если величина перегрузки не превышает 5%, то надежность конструкции считается достаточной.

Площадь сечения: A_шв = 4* A_табл, [1, стр. 54] (8.8)

где A_шв – площадь сечения швеллера [см²]; A_табл – площадь сечения швеллера по таблице сортамента [см²].

A_шв = 4*53.4 = 213.6 см².

По таблице сортамента таблице сортамента выбирается двутавр

№ 40К2:

= , [1, стр. 54] (8.9)

где – момент сопротивления сечения [см³]; – момент сопротивления сечения по таблице сортамента [см³].

= 1067 см³,

Площадь сечения: A_дв = A_табл, [1, стр. 54] (8.10)

где A_дв – площадь сечения двутавра [см²]; A_табл – площадь сечения двутавра по таблице сортамента [см²].

A_дв = 210.96 см².

Наиболее рациональным является сечение, имеющее наименьшую площадь поперечного сечения: двутавр A_дв = 210.96 см², швеллер A_шв = 213.6 см², прямоугольник A_пр = hb =14.42*7.21 = 103.97 см², круг A_кр = = = 146.48 см².

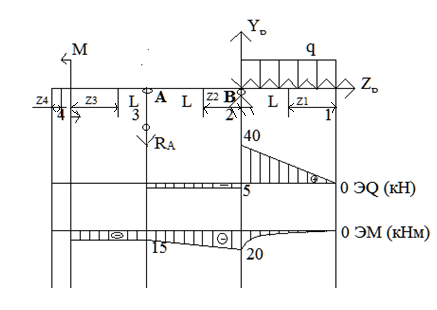
Рис.8

Задача 9. Построение упругой линии балки.

Требуется составить дифференциальное уравнение упругой линии балки, определить постоянные интегрирования, рассчитать углы поворота на опорах и прогиб в середине пролета балки, построить изогнутую ось балки.

Исходные данные:

М = 25 кНм; q = 20 кН/м; F = 45 кН; L = 10м.