6.5 Проверка полученных результатов.

С целью проверки выполненного расчета определяются деформации стержней:

Δl₁ = = = 2.84*10^-5 м = 0.0284 мм;

Δl₂ = = = 4.14*10^-5 м = 0.0414 мм;

Δl_t = α_t*Δt*l₂, [1, стр. 35] (6.5)

где Δl_t – температурное удлинение стержня в свободном состоянии [мм]; α_t – коэффициент линейного растяжения [1/˚С]; Δt – величина нагрева стержня 2 [˚С]; l₂ – длина стержня 2 [мм].

Δl_t = 229*10^-7*30*0.15 = 0.103 мм.

Δl₂ = Δl_t –2.19Δl₁; 0.0414 = 0.103 – 2.19*0.0284;

0.0414 = 0.103 – 0.062; 0.0414 = 0.041.

Небольшое расхождение вызвано округлением значений в ходе расчета.

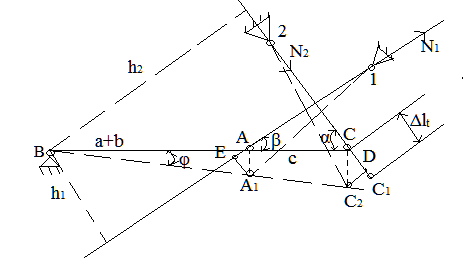
Рис. 6

Задача 7. Расчет круглого вала на прочность и жесткость при кручении

Исходные данные:

Вал защемлен одним концом и загружен внешними скручивающими моментами Материал вала – сталь 3, модуль сдвига , допускаемое касательное напряжение , допускаемый относительный угол закручивания

1. Построение эпюры крутящих моментов Т₂.

Используем метод сечений. Вал разбивается на четыре силовых участка (рис.9,а). Крутящий момент в каждом сечении определяется как алгебраическая сумма внешних скручивающих моментов, взятых по одну сторону от сечения. Правило знаков для моментов принимаем произвольно. Расчет ведем со свободного конца вала.

1-й участок:

0 ≤ z₁ ≤ 0,1м

.

2-й участок:

0 ≤ z₂ ≤ 0,1м

.

3-й участок:

0 ≤ z₃ ≤ 0,3м

.

4-й участок:

0 ≤ z₄ ≤ 0,2м

По полученным данным строится эпюра крутящих моментов (рис.9,б).

2. Расчет диаметра вала.

На основание эпюры выбирается максимальное значение крутящего момента:

I-я ступень

- из условия прочности,

- из условия жесткости.

II -я ступень

- из условия прочности,

- из условия жесткости.

За окончательные принимаются большие диаметры:

1. Построение эпюры улов закручивания.

Предварительно определяем полярный момент инерции сечения:

Определяем угол закручивания в сечениях a, b, c, d, e, начиная от закрепленного торца:

Сечение a не поворачивается, т.е. угол поворота

Угол поворота сечения b относительно неподвижного сечения a равен углу закручивания на участке ab:

Угол поворота сечения с относительно неподвижного сечения a складывается из угла поворота сечения b и угла закручивания на участке bc:

Угол поворота сечения d относительно неподвижного сечения a складывается из угла поворота сечения c и угла закручивания на участке cd:

Сечение d не поворачивается, так как =0, следовательно

По полученным значениям строится эпюра углов закручивания. Поскольку на участках нет распределенной скручивающей нагрузки, эпюра будет прямолинейной (рис 9, в).

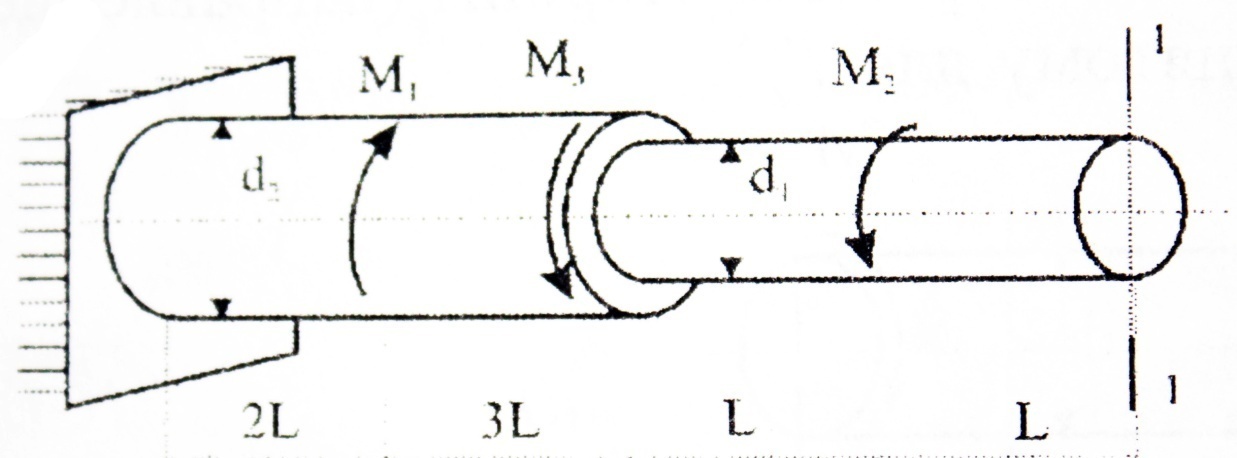
Задача 8. Построение эпюр внутренних силовых факторов в балке при изгибе.

Требуется построить эпюры внутренних силовых факторов Q и М в балке и подобрать размеры поперечных сечений разной формы (круг, прямоугольник, швеллер, двутавр) из условия прочности по нормальным напряжениям.

Исходные данные:

M = 15кНм; q = 40 кН/м; L = 1м; [σ] = 160 МПа.