5.1 Статическая часть.
Возникновение монтажных напряжений обусловлено тем, что при монтаже конструкции, элементы которой имеют отклонения от номинальных размеров, конструкция и ее элементы деформируются. Возникающие при этом напряжения называются монтажными.
Для правильной оценки надежности конструкции необходимо знать не только рабочие, но и монтажные напряжения. Для решения данной задачи система изображается в деформированном состоянии без внешней нагрузки. Предполагаем, что стержень 1 короче на величину δ, то после сборки конструкции стержень 1 окажется растянутым на величину Δl1, жесткий стержень – повернутым против часовой стрелке относительно шарнира В, в результате чего стержень 2 окажется сжатым на величину Δl2.
Составляется уравнение равновесия для недеформируемой стержневой системы, считая ее рычагом с шарнирным закрепление в точнее В:
0; h1 = с*sinβ; h2 = b*sinα.
– N2*b*sinα + N1*c*sinβ = 0
N1*c*sinβ = N2*b*sinα
N1*1.3*0.5 = N2*1.9*√2/2
N1= 2.06N2 (5.1)
5.2 Геометрическая часть задачи.
Для получения дополнительного уравнения необходимо геометрически связать между собой деформации стержней Δl1, Δl2.
CЕ = Δl1; AD = Δl2; AA1 = ; CC1 =
Δl2
= AA1*
sinα;
AA1
=
;
CC1
=
=
;
φ
= 
;
;
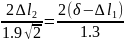1.3Δl2
= 2.69
(δ
–Δl1);
Δl2 = 2.06 (δ –Δl1) – уравнение совместности деформаций.
Полученное уравнение отражает соотношение деформаций стрежней 1, 2. Для использования полученного выражения совместно с уравнением (5,1) необходимо перейти от деформаций к усилиям в стержнях.
5.3 Физическая часть задачи.
Для преображения уравнения совместности деформаций используют закон Гука [1, стр. 30]:
Δl1 = ; Δl2 = , (5.2)
где Δl – деформация [м]; N – внешнее усилие в стержне [кН]; l – длина стержня [м]; A – площадь сечения стержня [м2]; Е – модуль упругости [МПа].
5.4 Синтез уравнений.
Подставляем выражения закона Гука в уравнение совместности деформаций, получим:
= 2.06(δ – ).
Подставляя значения и переводя модули в кПа, получим:
=2.06*0.05*10-3
– 2.06*
;
0.36*10-5N2 = 0.103*10-3 – 0.23* 10-5 N1;
N2 = 0.03 – 0.64 N1 (5.3)
Уравнения (5.1) и (5.3) образуют систему взаимосвязанных уравнений:
;
N1
= 2.06(0.03 – 0.6N2);
2.32 N1 = 0.062; N1 = 0.027 кН; N2 = 0.03 – 0.64*0.027 = 0.013 кН.
После определения усилий рассчитываются монтажные напряжения в стержнях [1, стр. 31]:
σ = N/A, (5.4)
где σ – напряжение на стержнях [МПа]; N – внешнее усилие на стержне [кН]; A – площадь сечения стержня [м2].
σ1 = N1/A1 = 0.027*103/0.44*10-3 = 0.061 МПа;
σ2 = N2/A2 = 0.013*103/0.59*10-3 = 0.022 МПа.
Результаты расчета показывают, что даже при незначительном отклонении от размеров при монтаже могут возникать весьма существенные монтажные напряжения, не учет которых может значительно снизить надежность конструкции или даже привести к выходу ее из строя.
5.5 Проверка полученных результатов.
С целью проверки выполненного расчета определяются деформации стержней:
Δl1
=
=
=
0.003*10-5
м = 0.03 мм;
Δl2
=
=
= 0.004*10-5
м = 0.04 мм;
Δl2 = 2.06 (δ –Δl1); 0.04 = 2.06(0.05 – 0.03) = 0.04;
0.04 = 0.04.
Небольшое расхождение вызвано округлением значений в ходе расчета.
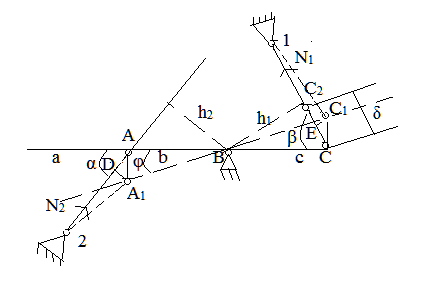
Рис. 5
Задача 6. Расчет температурных напряжений в статически неопределимых конструкциях.
Требуется рассчитать температурные напряжения в стержнях 1, 2, вызванные нагревом стержня 2.
Исходные данные:
α = 45˚; β = 30˚; a = 1.3 м; b = 1.8 м; с = 1.7 м; n = 0.75; l1 = 0.1 м; l2 = 0.15 м; A1 = 0.44*10-3 м2; A2 = 0.59*10-3 м2; Е1 = 2*105 МПа; Е2 = 0.7*105 МПа;
Δt = 30˚C – величина нагрева стержня 2; αt1 = 125*10-7 1/˚C; αt2 = 229*10-7 1/˚C.