4.1 Статическая часть задачи.
В результате действия внешней нагрузки жесткий стержень повернется относительно шарнира В по часовой стрелки. Таким образом, стержень 1 испытывает растяжения, а стержень 2 – сжатие.
Составляются уравнения равновесия для недеформированной системы:
0;
h2
= a*sinα;
h1
= (a + b)sinβ.
– q*a*(a/2) – F(a + b + c) + N2*a*sinα + N1(a + b)sinβ = 0
– 40*1.42/2 – 25(1.4 + 1.9 + 1.3) + N2*1.4*√2/2 + N1(1.4 + 1.9)1/2= 0
0.55N1 = 51.4 – 0.33N2 (4.1)
В полученном уравнении два неизвестных усилия N1 и N2. Для его решения необходимо составить еще одно уравнение с неизвестными усилиями , чтобы количество неизвестных стало равно числу уравнений.
4.2 Геометрическая часть.
Система изображается в деформированном состоянии. Все точки жесткого стержня поворачиваются относительно опоры В на один и тот же угол. При выполнении данной части используются следующие допущения:
– искажением углов при деформации пренебрегают;
– считают, что точки жесткого стержня при его повороте перемещаются не по дугам, а по перпендикулярам к радиусам вращения.
На расчетной схеме определяются отрезки, изображающие деформации стержней Δl1, Δl2. Для этого из конечного положения точек A и C стержней опускается перпендикуляр на ось стержня до его деформации.
АЕ =
Δl1;
СD
= Δl2;
AA1
=
;
CC1
=
;
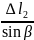φ
=
;
3.3Δl1 = 1.9Δl2;
Δl1 = 0.6Δl2 – уравнение совместности деформаций.
4.3 Физическая часть.
Для преобразования уравнения совместности деформаций используется закон Гука [1, стр. 26]:
Δl1
=
;
Δl2
=
, (4.2)
где Δl – деформация [м]; N – внешнее усилие в стержне [кН]; l – длина стержня [м]; A – площадь сечения стержня [м2]; Е – модуль упругости [МПа].
4.4 Синтез уравнений.
Подставляем выражения закона Гука в уравнение совместности деформаций, получим:
= 0.6 .
Учитывая, что A1/A2 = 0.75, преобразуем полученное выражение:
=0.6
;
N1 =1.9 N2. (4.3)
Уравнения (4.1) и (4.3) образуют систему взаимосвязанных уравнений:
,
при решении которой определяются решении в стержнях:
0.55*1.9N2 = 51.4 – 0.33N2
1.045N2 = 51.4 – 0.33N2
1.375N2 = 51.4
N2 = 37.38 кН; N1 = 1.9*37.38 = 71.02 кН.
4.5 Расчет диаметров стержней.
В одном из стержней напряжения принимаются равными допускаемой величине и площадь определяется из условия прочности [1, стр. 26]:
A1 = N1/[σ]1, (4.4)
где A – площадь сечения стержня [м4]; N – внешнее усилие в стержне [кН]; [σ] – допустимое напряжение [МПа].
A1 = 71.02*103/(160*106) = 0.44*10-3 м2.
Площадь сечения второго стержня определяется по заданному соотношению:
A2 = A1/0.75 = 0.44*10-3/0.75 = 0.59*10-3 м2.
Производится проверка этого стержня по условию прочности
[1, стр. 27 ]:
σ ≤ [σ] (4.5)
где σ – напряжение на стержнях [МПа]; [σ] – допустимое напряжение на стержнях [МПа].
σ2 = N2/A2 , [1, стр. 27] (4.6)
где σ – напряжение на стержнях [МПа]; N – внешнее усилие на стержне [кН]; A – площадь сечения стержня [м2].
σ2 = 37.38*103/0.59*10-3 = 63.36 МПа ≤ [σ] – условие прочности выполняется.
Рассчитывается диаметры стержней [1, стр. 27]:
d1
=
, (4.6)
где d – диаметр стержня [мм]; А – площадь сечения стержня [м2].
d1
=
= 2.37 *10-2
м = 0.237 мм;
d2
=
= 2.74*10-2
м =0.274 мм.
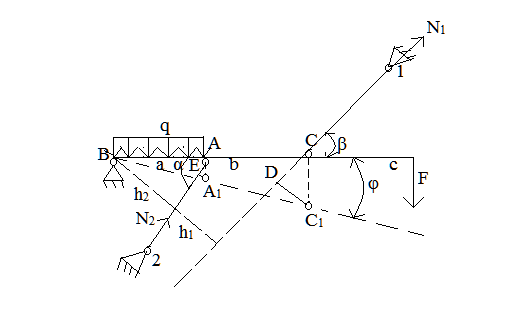
Рис. 4
Задача 5. Расчет монтажных напряжений в статически неопределимых конструкциях.
Требуется рассчитать монтажные напряжения в стержнях 1, 2, вызванные неточностью изготовления стержня 1.
Исходные данные:
α = 45˚; β = 30˚; a = 1.4 м; b = 1.8 м; с = 1.3 м; n = 0.75; l1 = 0.1 м; l2 = 0.15 м; A1 = 0.44*10-3 м2; A2 = 0.59*10-3 м2; Е1 = 2*105 МПа; Е2 = 0.7*105 МПа;
δ = 0.55 мм – неточность изготовления стержня 1.