3.1 Построение эпюры крутящих моментов Tz.

Используется метод сечений. Вид разбивается на три силовых участка. Крутящий момент в каждом участке определяется как алгебраическая сумма внешних скручивающих моментов, взятых по одну сторону от сечения. Расчет ведется от свободного конца вала.

1 – й участок.

Т₁ = М₃ = 1.3 кНм.

2 – й участок.

Т₂ = М₃ – M₂ = 1.3 – 3.5 = – 2.2 кНм.

3 – й участок.

Т₃ = М₃ – M₂ – M₁ = 1.3 – 3.5 – 2.3 = – 4.5 кНм.

По полученным данным строится эпюра крутящих моментов T_z.

3.2 Расчет диаметра вала.

На основании эпюры выбирается максимальное значение крутящего момента. Определяется диаметр вала:

Ступень 1.

|Т_max1| = 2.2 кНм.

, [1, стр. 106] (3.1)

где – диаметр вала из условия прочности [мм]; – максимальное значение крутящего момента [кН]; – допускаемое касательное напряжение [МПа].

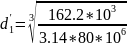
= 0.052 м = 52 мм – из условия прочности.

, [1, стр. 106] (3.2)

где – диаметр вала из условия жесткости [мм]; G – модуль сдвига [МПа]; – допускаемый относительный угол закручивания [град/м].

= 0.0855 м = 86 мм – из условия прочности.

За окончание принимается больший диаметр, т.е. d₁ = = 86 мм.

Ступень 2 (рассчитываем по формулам (3.1) и (3.2)).

|Т_max2| = 4.5 кНм.

= 0.066 м = 66 мм – из условия прочности.

= 0.1023 м = 102 мм – из условия прочности.

За окончание принимается больший диаметр, т.е. d₂ = = 102 мм.

3.2 Построение эпюры углов закручивания.

Предварительно определяется полярный момент инерции сечения

[1, стр. 106]:

, (3.3)

где – полярный момент инерции сечения [м⁴]; – диаметр вала [мм].

= 4*10^-6 м⁴.

= = 11*10^-6 м⁴.

Определяем угол закручивания в сечениях a, b, c, k, начиная от закрепленного торца.

φ_a = 0, т.к. сечение а не поворачивается.

Угол поворота сечения b относительно неподвижного сечения а равен углу закручивания на участке ab [1, стр. 106]:

φ_b = φ_ab = , (3.4)

где φ_b – угол поворота сечения b [рад]; Т – крутящий момент на участке [кН]; l – длина участка [м]; I – полярный момент инерции сечения [м⁴].

φ_b = = – 128*10^-4 рад.

Угол поворота сечения с относительно неподвижного сечения а складывается из угла поворота сечения b и угла закручивания на участке bc:

φ_c = φ_b + φ_bc = φ_b + = –128*10^-4 + = –128*10^-4 – 34.4*10^-4 = – 162.4*10^-4 рад.

Угол поворота сечения k относительно неподвижного сечения а складывается из угла поворота сечения с и угла закручивания на участке ck:

φ_k = φ_c + φ_ck = φ_c + = –162.4*10^-4 + = –162.4*10^-4 + 61*10^-4 = – 101.4*10^-4 рад.

По полученным значениям строится эпюра углов закручивания.

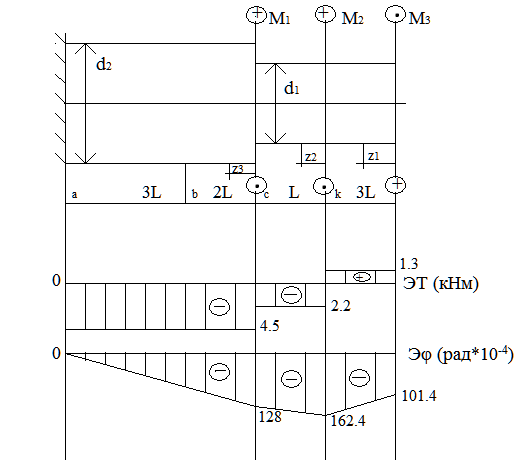
Рис. 3

Задача 4. Расчет статически неопределимой стержневой системы.

Требуется рассчитать диаметры стержней 1, 2(d₁, d₂) из условия прочности.

Исходные данные:

F =25 кН; q = 40 кН/м; α = 45˚; β = 30˚; a = 1.4 м; b = 1.8 м; с = 1.3 м; n = 0.75; l₁ = 0.1 м; l₂ = 0.15 м; A₁/A₂ = 0.75; [σ]₁ = 160 МПа; Е₁ = 2*10⁵ МПа; [σ]₂ = 130 МПа; Е₂ = 0.7*10⁵ МПа.