1.3 Построение эпюры нормальных напряжений.

При построении эпюры σ последовательно рассматриваются сечения стержня, в которых происходит скачкообразное изменение продольной силы или площади поперечного сечения.

= 0; [1, стр. 18] (1.5)

где σ – нормальное напряжение [МПа]; N – продольная сила [кН]; A – площадь поперечного сечения [м²].

= = 85 МПа;

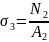= = 85 МПа;

= = –305 МПа.

По полученным значениям строится эпюра нормальных напряжений σ. 1.4 Построение эпюры перемещений.

1 – й участок.

Δl₁ = , [2, стр. 25] (1.6)

где Δl₁ – деформация участка 1[м]; E – продольный модуль упругости [МПа]; qz₁ – равнодействующая равномерно распределенной нагрузки, действующая на участке 1[кН].

Δl₁ = = = = 0.14*10^-3 м.

2 – й участок.

Δl₂ = , [1, стр.18] (1.7)

где Δl₂ – деформация участка 2 [м]; N – продольная сила [кН]; l – длина участка на котором действует сила [м].

Δl₂ = = 0.38 *10^-3 м.

3 – й участок.

Δl₃ = = -0,85*10^-3 м.

Рис.1

Задача 2. Определение геометрических характеристик составного симметричного сечения из стандартных профилей.

Требуется для симметричного сечения из стандартных профилей определить положение центра тяжести сечения, главные центральные моменты инерции I_Xc , I_Yc и момента сопротивления W_X относительно оси изгиба X.

Исходные данные (принимаются из таблиц сортамента):

швеллер № 24:

= 240 мм = 24 см; = 90 мм = 9 см; s₁ = 5.6 мм = 0.56 см; t₁ = 10 мм = 1 см; z₀ = 2.42 см; A₁ = 30.6 см²; I_X1= I_Y^табл = 208 см⁴; I_Y1= I_X^табл = 2900 см⁴.

неравнобокий уголок №11/7:

B₂ = 110 мм = 11 см; b₂ = 70 мм = 7 см; d₂ = 6.5 мм = 0.65 см; A₂ = 11.4 см²; x₂ = 1.58 см; y₂ = 3.55 см; I_X2= 142см⁴; I_Y2= 45,6 см⁴.

толщина стального листа t = 10 мм.

2.1 Определение положения центра тяжести сечения.

Сечение разбивается на простые фигуры 1 (швеллер), 2 (уголок), 3 (прямоугольник), в фигурах проводятся центральные оси, выбирается исходная система координат Y'X'. В качестве исходных осей можно использовать центральные оси одной из фигур (например, прямоугольник). Так как вертикальная ось является осью симметрии фигуры, то она будет главной центральной осью сечения Y_С. Поэтому необходимо определить положение второй главной центральной оси X_С, т. е. положение центра тяжести сечения на оси Y_С.

Определяются координаты центров тяжести фигур по исходной оси Y' (с учетом знака):

для швеллера: 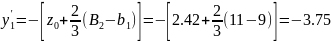см;

для уголка: см;

для прямоугольника (так как вспомогательные оси проходят через центр тяжести этой фигуры).

Определяется площадь сечения [1, стр.41]:

A = A₁ + 2A₂ + 2A₃ (2.1)

где A₁ – площадь сечения швеллера [м²]; A₂ – площадь сечения равнобокого уголка [м²]; A₃ – площадь сечения прямоугольника [м²].

А = 30.6 см² + 2*11.4 см² + 2*25.3 см² = 104 см²

Определяются статические моменты фигур относительно исходной оси X' [1, стр. 42]:

(2.2)

где – статический момент фигуры [см]; Аⁱ – площадь сечения фигуры [см²]; – координаты центров тяжести фигур по исходной оси Y'[см].

см;

см;

(так как вспомогательные оси совпадают с центральными осями фигуры).

Определяется координата центра тяжести сечения в исходной оси Y' [1, стр. 41]:

, (2.3) где – координата центра тяжести сечения в исходной оси Y' [см]; - статические моменты швеллера, уголка, прямоугольника [см]; А – площадь сечения фигуры [см²].

= (-11.4 – 65.66 + 0)/104 = –1.73 см.

Отмечается положение центра тяжести сечения на схеме и проводится главная центральная ось сечения X_C.

2.2 Определение осевых моментов инерции сечения относительно главных центральных осей [1, стр. 42].

, (2.4)

где – момент инерции фигуры [см⁴]; – момент инерции фигуры относительно собственной центральной оси [см⁴]; – площадь сечения фигуры [см²]; – координата центра тяжести сечения в исходной оси Y'[см]; – координаты центров тяжести фигур по исходной оси Y'[см].

для швеллера: = 208 + 30.6(1.73g – 3.75)² = 332.86 см⁴;

для уголка: = 142 + 11.4(1.73 –2.88)² = 157.08 см⁴;

для прямоугольника:

см⁴.

Момент инерции всего сечения равен:

относительно оси X_C [1, стр. 42]:

, (2.5)

где – момент инерции сечения относительно оси X_C [см⁴]; – моменты инерции швеллера, уголка, прямоугольника [см⁴].

= 332.86 + 2*157.08 + 2*77.82 = 802.66 см⁴.

относительно оси Y_C [1, стр. 43]:

, (2.6)

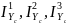где – момент инерции сечения относительно оси Y_C [см⁴]; – моменты инерции швеллера, уголка, прямоугольника [см⁴].

= I_X^табл = 2900 см⁴;

= 45.6 + 11.4(2 + 0.65 – 1.58)² = 1442.6 см⁴; 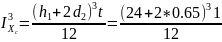= 1349.5 см⁴;

= 2900 + 2*1443.6 + 2*1349.5 = 8484.2 5 см⁴.

2.3 Определение моментов сопротивления [1, стр. 43].

, , (2.7)

где , - моменты сопротивления относительно главных осей [см³]; , - моменты инерции сечения относительно главных осей [см⁴]; , – расстояние от наиболее удаленной точки сечения до соответствующей нейтральной (главной) оси [см].

= (3.75 – 1.73) + (9 – 2.42) = 8.6 см; = 12.65 см.

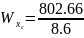= 93.33 см³;

= 670.69 см³ .

Рис. 2

Задача 3. Расчет круглого ступенчатого вала на прочность и жесткость при кручении.

Требуется построить эпюру крутящих моментов, определить из условий прочности и жесткости диаметр вала, построить эпюру абсолютных углов закручивания сечений по отношению к неподвижному сечению в заделке.

Исходные данные:

M₁ = 2.3 кНм; M₂ = 3.5 кНм; M₃ = 1.3 кНм; L= 0.5 м; [τ] = 80 МПа;

[θ˚] = 0.3 град/м; G = 0.8*10⁵ МПа.