9.Уравнение Шредингера (уш).
Развивая
идеи де Бройля, Шредингер сопоставил
им движущуюся комплекснозначную функцию
координат от времени
- волновую или пси-функцию, котораяполностью
характеризует состояние микрочастицы
и содержит всю информацию о её движении.
УШ
–основное уравнение квантовой механики,
оно не выводится, а постулируется.
Справедливость УШ доказывается тем,
что выводы, следующие из него, согласуются
с экспериментальными данными. УШ:
.
Когда
состояние частицы можно считать
независимым от времени, для её описания
можно воспользоваться стационарным
УШ:
.
19.Проходжения частицы через потенциальный барьер.
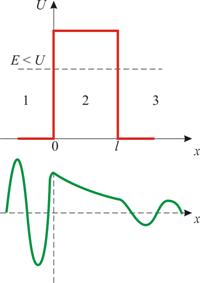
Потенциальный барьер – это область пространства, разделённая на 2 области различными потенциальными энергиями, характеризуется высотой – минимальной потенциальной энергией классической частицы, необходимой для преодоления барьера.
Рассмотрим
простейший потенциальный барьер
прямоугольной формы для одномерного
(по оси х)
движения частицы: для микрочастицпри E < U,
имеется отличная от нуля вероятность,
что частица отразится от барьера и будет
двигаться в обратную сторону.
При E > U имеется
также отличная от нуля вероятность, что
частица окажется в области x > l,
т.е. проникнет сквозь барьер. Такой вывод
следует непосредственно из решения
уравнения Шредингера, описывающего
движение микрочастицы при данных
условиях задачи:
.
Туннельный эффект – явление проникновения частицы через потенциальный барьер. Коэффициент прозрачности D – вероятность проникновения частицы через барьер, чем больше ширина – тем меньше вероятность проникновения.
Билет №6
Комбинационное рассеяние света (эффект Рамана) — неупругое рассеяние оптического излучения на молекулах вещества (твёрдого, жидкого или газообразного), сопровождающееся заметным изменением частотыизлучения. В отличие от рэлеевского рассеяния, в случае комбинационного рассеяния света в спектре рассеянного излучения появляются спектральные линии, которых нет в спектре первичного (возбуждающего) света. Число и расположение появившихся линий определяется молекулярным строением вещества.
С точки зрения классической теории
Данная точка зрения даёт несколько упрощённую картину явления. В классической модели электрическое поле света индуцирует переменный дипольный моментмолекулы, который колеблется с частотой падающего света, а изменения дипольного момента в свою очередь приводят к испусканию молекулой излучения во всех направлениях. В классической модели принимается, что вещество содержит заряды, которые могут быть разделены, но удерживаются вместе некоторыми силами, действующими наряду с кулоновским притяжением. Образование волны на границе с веществом вызывает осциллирующее разделение этих зарядов, то есть появляется осциллирующий электрический диполь, который излучает на частоте осцилляции. Это излучение и является рассеянием. Выражение для интенсивности излучения имеет вид
С точки зрения квантовой теории
Иллюстрация
Происхождение данного эффекта удобнее всего объяснить в рамках квантовой теории излучения. Согласно ей, излучение частоты ν рассматривается как поток фотонов с энергией hν, гдеh — постоянная Планка. При столкновениях с молекулами фотоны рассеиваются. В случае упругого рассеивания, они будут отклоняться от направления своего движения, не изменяя своей энергии (Рэлеевское рассеяние).
Теплоемкость кристаллической решетки
, количество которых определяется распределением Больцмана:Носителями энергии равновесного теплового излучения согласно концепции Планка являются стоячие (электромагнитные) волны. При этом энергия для каждой частоты отмеряется “порциями”, квантами ћ
.
И весьма интересно, что в совсем другой задаче, задаче о теплоемкости кристаллической решетки опять-таки “проходит” такой же подход.
Однако, сначала нужно сказать несколько слов об истории вопроса. Содержащий N атомов кристалл имеет 3N степеней свободы - столько значений координат необходимо для описания положения атомов. Согласно классическим представлениям на каждую степень свободы должна приходиться энергия kT: по kT/2 на кинетическую и на потенциальную энергию. Отсюда следует закон Дюлонга и Пти, согласно которому молярная теплоемкость Cm всех кристаллов одинакова:
.
Здесь NA - число Авогадро, R - универсальная газовая постоянная.
Билет №7
37. Тождественные частицы. Симметричные и антисимметричные состояния. Фермионы и бозоны. Фазовое пространство. Квантовые распределения Ферми-Дирака и Бозе-Эйнштейна.
Тожд. частицы - имеют одинаковые св-ва. Принцип о неразл. ТЧ: сост. сис-мы, получ. друг из друга перестановкой ТЧ местами, неразличимы и должны рассм. как одно физ. сост. 2 типа волн. ф-ций: симметричные(не меняю знак при перестановке - бозоны(фотоны,фононы)) и антисимм.(меняют знак - фермионы(электроны,протоны)). Для опис.сост. квантовой сис-мы тожд.частиц рассм. 6-тимерное фазовое пр-во(мю пр-во) с осями x,y,z,px,py,pz Изменение с течением t изобр-ся движением точки вдоль фазовой траектории. Состоянию частицы в мю-пр-ве сооств. ячейка фазового пр-ва объемом dЛ=dxdydzdpxdpydpz~=h^3.
f(ei)-ф-ция заселенности ячеек, вер-ть того что в сост.тепл.равновесия идеального газа при T состояние с энерг.ei занято частицей. Для фермионов f(ei)=1/(exp(ei-мю)/(kT)+1) - распр. Ферми-Дирака, для бозонов f(ei)=1/(exp(ei-мю)/(kT)-1) - распр. Бозе-Эйнштейна.
Особ-ти: 1.для ферм.f(ei)<=1, для боз.f(ei)>=0
2. усли f<<1 то f(ei)=exp(мю-ei)/(kT)=Aexp(-ei/(kT)) - распр.Больцмана
3. в макросис-ме энерг.уровни дискретны, но расположены густо => в формулах опред.ei индекс i можно опустить
4. для бозонов мю<=0
dЛ/h^3=dZ-число фазовых ячеек