17. Средняя квадратическая погрешность среднего арифметического значения.

Оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений.

В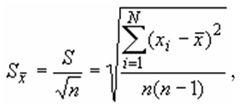 ычисляется по формуле

где S - средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; n - число единичных измерений в ряду.

Формула показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза.

18. Средняя квадратическая погрешность вероятнейшего значения.

19. Средняя квадратическая погрешность функции измеренных величин.

Пусть u = f(X,Y,Z) есть некоторая функция независимых величин X, Y, Z, измеренных или вычисленных со средними квадратическими ошибками mx, my, mz.

Продифференцируем функцию по всем переменным и получим

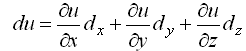
В этой формуле бесконечно малые приращения – дифференциалы – заменим истинными ошибками. Получим выражение

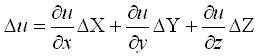
Перейдем от истинных ошибок к средним квадратическим ошибкам. Для этого положим, что X, Y, Z измерено n раз, где можно считать . Соответственно числу измерений составляем n равенств

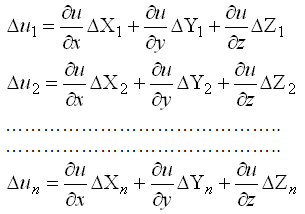
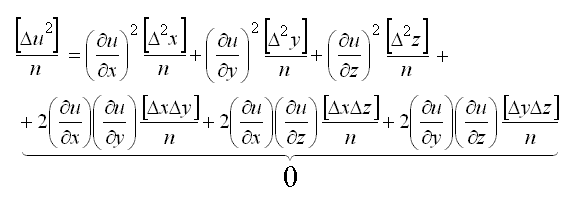
Возведем каждое из равенств в квадрат, сложим и разделим на n

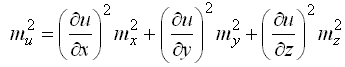
А так как

Пример 1.Определить СКП превышения, полученного по формуле h=d. tgν, если горизонтальное проложение d=100.0 м, ν=4? 30', md=0.5 м, mν=1'.

Решение.

1.Находим частные производные

dh/dd = tgν, dh/dv=d/cos2ν.

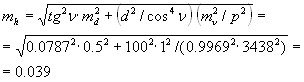
20. Почему точность измерений оценивают средней квадратичной погрешностью а не средней арифметической.

21. Заложение. Масштаб заложений. Высота сечения рельефа. Уклон. Наклон.

Заложением называется расстояние между смежными горизонталями на топографической карте, зависящее от принятой высоты сечения рельефа на данной карте и крутизны ската в данном месте.

Заложение является проекцией линии ската на горизонтальную плоскость. Шкала заложений помещается на каждом листе топографических карт масштабов 1 : 200 000 и крупнее.

Построение шкалы заложений выполняется следующим образом. Составляют список значений углов α наклона линий на скате для принятой высоты h сечения рельефа данной карты. Для каждого угла наклона α вычисляют значение заложения d в масштабе данной карты по формуле d = h ctgα.

Создают, проведя горизонтальную линию, основание шкалы заложений, являющееся осью углов наклона линий на скате. Вдоль основания шкалы заложений от его левого края в произвольном масштабе откладывают отрезки, длина которых кратна выбранным значениям углов наклона линий на скате. В конце каждого отрезка проводят линию, перпендикулярную к основанию шкалы заложений, и вдоль нее откладывают заложение d, вычисленное для данного угла наклона α. При этом в начале основания шкалы заложений (его левом крае) откладывают заложение для минимального значения угла наклона. Через верхние концы отложенных заложений проводят плавную кривую шкалы заложений. Напротив нижних концы отложенных заложений под основанием шкалы заложений записывают значения соответствующих углов наклона α. Над шкалой заложений записывают значение высоты h сечения рельефа.

Р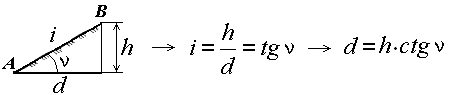 азность высот смежных горизонталей называется высотой сечения рельефа и обозначается буквой h.

Определение уклона и угла наклона ската

Уклоном линии местности называют отношение превышения к горизонтальному проложению.

Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона ската.