формула Уилсона, EOQ-модель.

Формула оптимального размера заказа для единственного продукта может быть представлена как точка минимума следующей функции издержек:

Общие издержки = издержки на закупку + издержки размещения заказа + издержки хранения,

что соответствует:

Продифференцировав обе части уравнения и приравняв выражение к нулю, получим:

В результате получим:

Решим относительно Q:

Знак (*) означает оптимальный размер заказа

Теория игр — это раздел математической экономики, изучающий решение конфликтов между игроками и оптимальность их стратегий. Конфликт может относиться к разным областям человеческого интереса: чаще всего это экономика, социология, политология, реже биология, кибернетика и даже военное дело. Конфликтом является любая ситуация, в которой затронуты интересу двух и более участников, традиционно называемых игроками. Для каждого игрока существует определенный набор стратегий, которые он может применить. Пересекаясь, стратегии нескольких игроков создают определенную ситуацию, в которой каждый игрок получает определенный результат, называемый выигрышем, положительным или отрицательным. При выборе стратегии важно учитывать не только получение максимального профита для себя, но так же возможные шаги противника, и их влияние на ситуацию в целом.

Равновесие Нэша (англ. Nash equilibrium) названо в честь Джона Форбса Нэша — так в теории игр называется тип решений игры двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив своё решение в одностороннем порядке, когда другие участники не меняют решения. Такая совокупность стратегий выбранных участниками и их выигрыши называются равновесием Нэша

Типы игр

Кооперативная\некооперативная игра

Кооперативной игрой является конфликт, в котором игроки могут общаться между собой и объединяться в группы для достижения наилучшего результата. Примером кооперативной игры можно считать карточную игру Бридж, где очки каждого игрока считаются индивидуально, но выигрывает пара, набравшая наибольшую сумму. Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом. Не смотря на то, что эти два вида противоположны друг другу, вполне возможно объединение стратегий, которое может принести больше пользы, чем следование какой-либо одной.

С нулевой суммой и с ненулевой суммой

Игрой с нулевой суммой называют игру, в которой выигрыш одного игрока равняется проигрышу другого. Например банальный спор: если вы выиграли сумму N, то кто-то эту же сумму N проиграл. В игре же с ненулевой суммой может изменяться общая цена игры, таким образом принося выгоду одному игроку, не отнимаю ее цену у другого. В качестве примера здесь отлично подойдут шахматы: превращая пешку в ферзя игрок А увеличивает общую сумму своих фигур, при этом не отнимая ничего у игрока Б. В играх с ненулевой суммой проигрыш одного из игроков не является обязательным условием, хотя такой исход и не исключается.

Параллельные и последовательные

Параллельной является игра, в которой игроки делают ходы одновременно, либо ход одного игрока неизвестен другому, пока не завершится общий цикл. В последовательной игре каждый игрок владеет информацией о предидущем ходе своего оппонента до того, как сделать свой выбор. И совсем не обязательно информации быть полной, что подводит на с кледующему типу.

С полной или неполной информацией

Эти типы являются подвидом последовательных игр, и названия их говорят сами за себя.

Метаигры

Эти игры являются «леммами» теории игр. Они полезны не сами по себе, а в контексте какого-либо конфликата, расширяя его набор правил. В любом конфликте типы объединяются, определяя таким образом правила игры, будь это кооперативная последовательная игра с нулевой суммой, или метаигра с неполной информацией.

Проблемы практического применения

Безусловно, следует указать и на наличие определенных границ применения аналитического инструментария теории игр. В следующих случаях он может быть использован лишь при условии получения дополнительной информации. Во-первых, это тот случай, когда у игроков сложились разные представления об игре, в которой они участвуют, или когда они недостаточно информированы о возможностях друг друга. Например, может иметь место неясная информация о платежах конкурента (структуре издержек). Если неполнотой характеризуется не слишком сложная информация, то можно применять опыт подобных случаев с учетом определенных различий. Во-вторых, теорию игр трудно применять при множестве ситуаций равновесия. Эта проблема может возникнуть даже в ходе простых игр с одновременным выбором стратегических решений. В-третьих, если ситуация принятия стратегических решений очень сложна, то игроки часто не могут выбрать лучшие для себя варианты. Например, на рынок в разные сроки могут вступить несколько предприятий или реакция уже действующих там предприятий может оказаться более сложной, нежели быть агрессивной или дружественной. Экспериментально доказано, что при расширении игры до десяти и более этапов игроки уже не в состоянии пользоваться соответствующими алгоритмами и продолжать игру с равновесными стратегиями. К сожалению, ситуации реального мира зачастую очень сложны и настолько быстро изменяются, что невозможно точно спрогнозировать, как отреагируют конкуренты на изменение тактики. Тем не менее, теория игр полезна, когда требуется определить наиболее важные и требующие учета факторы в ситуации принятия решений в условиях конкурентной борьбы. Эта информация важна, поскольку позволяет учесть дополнительные переменные или факторы, имеющие возможность повлиять на ситуацию, и тем самым повысить эффективность решения.

Виды задач и критерии выбора

Различают два вида задач в играх с природой:

• Задача о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний;

• Задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы;

Чтобы быть ближе к реальным ситуациям, для примера возьмем относительно реальную ситуацию. Первого игрока, за которого мы будем принимать решения, будет представлять Samsung со своим Galaxy S5. Вторым игроком, играющим «природу», будет компания Apple, и его iPhone 6. Подходит время выпуска нового смартфона, прошла презентация, эксперты высказали свое мнение, и игрок один должен принять важное решение, когда выпустить продукт? Упростив ситуацию, у нас останется три варианта: до конкурента (А₁), вместе с ним (А₂) или после (А₃). Естественно, пока не выйдет новый iPhone мы не узнаем, будет он намного лучше нашего (В₁), таким же (В₃) или сильно уступающим в качестве (В₃). Посчитав прибыль во всех случаях, в итоге получим матрицу:

	В1	В2	В3
А1	5	5	7
А2	3	4	6
А3	2	4	8

Теперь же, для принятия решения, у нас есть несколько критериев. 1. Критерий Вальда (максиминный). Игрок рассчитывает, что природа пойдет по наихудшему для него пути, и следует выбрать вариант с максимальной прибылью при самом плохом исходе, поэтому данный критерий считается пессимистическим. Представить его можно в виде max (min i) При данном критерии: для А₁ минимальной прибылью (5) выльются действия природы В₁ и В₂ для А₂ минимальная прибыль 3 после действия В₁ для А₃ минимальная прибыль 2 после действия В₁ Таким образом из 5, 3 и 2 максимум прибыли (5) нам даст вариант А₁ 2. Критерий максимума (максимаксный) является оптимистическим, т.е. мы надеемся на самый благоприятный для нас исход.представляется как max (max i). для А₁ максимальная прибыль 7 для А₂ максимальная прибыль 6 для А₃ максимальная прибыль 8 Из 7, 6 и 8 максимальную прибыль принесет вариант А₃ 3. Критерий Гурвица рекомендует стратегию, определяемую по формуле max (A*max i + (1-A)*min i), где А — степень оптимизма и изменяется в пределах от 0 до 1. Критерий выдает результат, учитывающий возможность как наихудшего, так и наилучшего поведения природы. При А=1 данный критерий можно заменить критерием максимума, а при А=0 — критерием Вальда. Величина А зависит от степени ответственности игрока один: чем она выше, тем ближе А к единице. Для данного примера примем А=0,4. для А₁ прибыль равна 0,4*7 + 0,6*5 = 5,8 для А₂ прибыль равна 0,4*6 + 0,6*3 = 4,2 для А₃ прибыль равна 0,4*8 + 0,6*2 = 4,4 Из полученных ответов максимыльную прибль приносит действие А₁ 4. Критерий Сэвиджа (минимаксный). Суть его заключается в выборе стратегии, не допускающей слишком высоких потерь. Для этого используется матрица рисков, в которой вычисляется максимальная прибыль при каждом варианте действия игрока, и среди результатов выбирается наименьший. Его формула выглядит как min (max i) При данном критерии: для А₁ максимальной прибылью (7) выльется действие природы В₃ для А₂ максимальная прибыль 6 после действия В₃ для А₃ максимальная прибыль 8 после действия В₃ Таким образом из 7, 6 и 8 минимум прибыли (6) нам даст вариант А₂ 5. По критерию Байеса предлагается придать равные вероятности всем рассматриваемым стратегиям, после чего принять ту из них, при которой ожидаемый выигрыш окажется наибольшим. Критерий имеет один недостаток: не всегда можно точно определить вероятность того или иного события со стороны природы. Формулой для него является max (Σ q*i). Сначала мы положили вероятность наступления каждого из собитий природы равной 0,33, и получили для А₁ 5*0,33 + 5*0,33 + 7*0,33 = 5,61 для А₂ 3*0,33 + 4*0,33 + 6*0,33 = 4,29 для А₃ 2*0,33 + 4*0,33 + 8*0,33 = 7,63 Очевидно что максимальную прибыль мы получим от варианта А₃. Однако, обратившись к экспертам, мы получили вероятности событий для природы 0,5; 0,4; 0,1; соответственно. Таким образом для А₁ 5*0,5 + 5*0,4 + 7*0,1 = 5,2 для А₂ 3*0,5 + 4*0,4 + 6*0,1 = 3,7 для А₃ 2*0,5 + 4*0,4 + 8*0,1 = 3,4 Думаю результат комментировать бессмысленно. Основная задача состоит в том, чтобы найти оптимальные (или хотя бы рациональные) стратегии, наилучшим образом приводящие систему к цели при заданных внешних условиях. Для выбора стратегий в условиях неопределенности можно применять любые критерии, в условиях риска действеннее критерий Байеса. Однако выбор между самими критериями основывается обычно на интуиции, зависит от характера принимающего решение (в частности, его склонности к риску). Если решение принимается в условиях неопределенности, то лучше использовать несколько критериев. В том случае, если рекомендации совпадают, можно с уверенностью выбирать наилучшее решение. Если рекомендации противоречивы, решение надо принимать более взвешенно, с учетом сильных и слабых сторон.

Принцип минимакса. Рассмотрим конечную игру двух лиц X и Y размерности mxn с нулевой суммой, т. е. Х имеет m стратегий , а Y n стратегий . Партия состоит в том, что Х и Y выбирают по одной из своих стратегий и , в результате чего платеж Х составляет величину , а платеж Y-- (игра с нулевой суммой). Составим следующую таблицу: Таблицу, задаваемую функцией целочисленных аргументов i=1,...,m и j=1,...,n , сопоставляющей паре стратегий и платеж , называют платежной матрицей игры, а игру, заданную платежной матрицей, называют игрой, приведенной к нормальной форме. В общем случае, решить игру—значит указать, какие стратегии из числа , и как часто следует применять каждому игроку, чтобы в среднем за большое число партий игроку Х максимизировать свой выигрыш, а игроку Y минимизировать свой проигрыш. Решение игр основывается на принципе минимакса, который состоит в следующем: какую бы стратегию ни выбрал игрок Х, игрок Y ответит такой стратегией , чтобы заплатить . Следовательно, игроку Х из всех своих стратегий нужно взять такую , которая обеспечивает . называется нижней ценой игры, а стратегия --минимаксной стратегией игрока Х. является гарантированным выигрышем игрока Х при любой стратегии игрока Y. С другой стороны, на всякую стратегию игрока Y сторона Х ответит стратегией , обеспечивающей . Следовательно, из всех надо выбрать такую , которая доставит . Величина называется верхней ценой игры , а --минимаксной стратегией игрока Y. Верхняя цена игры—это тот гарантированный уровень, больше которого Y не заплатит, если только он будет применять свою минимаксную стратегию , какие бы стратегии ни применяла сторона Х.

Учебный вопрос №1. СВЕДЕНИЕ РЕШЕНИЯ ИГРЫ К ЗАДАЧЕ ЛИНЕЙНОГО ПОРГРАММИРОВАНИЯ. На основании необходимого и достаточного условия нельзя непосредственно решить игровую задачу, но оно является необходимым теоретическим обоснованием. Сведем теперь решение игры к задаче ЛП. Имеем: 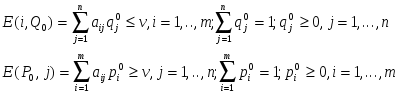(**) По сути дела, нахождение решения игры сводится к решению линейных неравенств: относительно неизвестных и . Причем величины и должны удовлетворять также условиям: Заметим, что, если к каждому элементу платежной матрицы прибавить константу C, то получим: Таким образом, необходимое и достаточное условие не изменилось, а следовательно, не изменились и оптимальные смешанные стратегии, в то время, как цена игры увеличилась на С. Поэтому выбором величины С всегда можно добиться, чтобы цена игры С была >0. Истинная цена игры найдется через как Введем новые переменные: Неравенства (**) запишутся в виде: Считаем, что лежит в окрестности , так что . Т. к. --непрерывна и Так как , то переходя к пределу при , получим: Если --оптимальные решения сопряженных задач ЛП,то , т. е. , а оптимальные с мешаные стратегии игроков выразятся как . Иначе говоря, у каждого игрока имеется, по крайней мере, чистая стратегия, которая, будучи применена против оптимальной смешанной стратегии противника, дает цену игры. По свойству оптимальных стратегий , следовательно, . Пусть , но тогда и подавно . Откуда , что противоречит тому, что --цена игры. Аналогично доказывается и второе равенство. Если для какого-либо выполняется , то в оптимальной смешанной стратегии , т. е. стратегия не участвует в оптимальном решении игрока X. Пусть , тогда , а так как для всех остальных , то получим . Пришли к противоречию. Аналогично, если для какого-либо выполняется , то в оптимальной смешанной стратегии величина .