Коэффициент запаса. Допускаемые напряжения.

Состояния, при которых происходят коренные изменения механического состояния материала в точке, называется предельным.

Различают два предельных состояния:

1) Переход материала в пластическое состояние, т.е. появление значительных остаточных деформаций.

2) Разрушение. Т.е. рост трещин и распадение на части.

Соответственно сказанному, оценивая состояние конструкции, различают два коэффициента запаса:

а) Коэффициент запаса по текучести где

- предел текучести;

- максимальное напряжение, возникающее в конструкции.

По данному коэффициенту оцениваются конструкции, выполненные из достаточно пластичных материалов.

б) Если материал конструкции хрупок и обладает незначительными пластическими свойствами, то прибегают к коэффициенту запаса по разрушению где

- предел прочности или временное сопротивление.

Иногда коэффициенты запаса выступают в другом качестве: в роли нормативных заданных величин, с помощью которых определяются так называемые допускаемые напряжения:

Допускаемое напряжение;

а) для пластичных материалов определяется

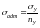
б) Для хрупких материалов

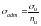
Расчет по методу допускаемых напряжений состоит в обеспечении условия: , называется условием прочности.

Статически неопределимые системы, работающие на растяжение и сжатие.

С истемы, у которых число неизвестных реакций связей превышает число независимых уравнений равновесия, называются статически неопределимыми системами.

В подобных случаях из уравнений статики не могут быть найдены внутренние силовые факторы, а, следовательно, и напряжения для всех элементов системы.

Например, стержень, защемленный одним концом -система статически определимая, однако, защемив второй конец стержня, мы получим систему статически неопределимую, т.к. неизвестных реакций станет 2, а уравнение равновесия, по-прежнему, единственное – сумма всех сил на ось стержня.

Стержневая система, состоящая из двух стержней, соединенных шарнирно – статически определима. Добавляя еще один стержень, мы превращаем ее в статически неопределимую, т.к. неизвестных усилия 3, а система сходящихся сил позволяет составить лишь два независимых уравнения статики.

Определить усилия в подобных системах, находясь в рамках гипотезы абсолютно твердого тела, принципиально невозможно. Выход из положения состоит в том, что нужно рассматривать деформации и перемещения, возникающие в системе.

Общий план решения статически неопределимых задач следующий:

1) Составляем уравнения равновесия.

2) Рассматривая перемещения узлов системы, составляем уравнения связывающие деформации отдельных элементов системы (или удлинения ее элементов). Эти уравнения называют обычно уравнениями совместности деформаций (совместности перемещений).

3) Заменяем в уравнениях совместности деформаций величины деформаций или удлинений через напряжения или усилия по зако-

ну Гука.

4) Решаем полученную линейную систему из уравнений равновесия и уравнений совместности и находим искомые усилия.